Aula 1: Relações Constitutivas

1. O que são Relações Constitutivas no Eletromagnetismo?

As relações constitutivas são o estudo da interação entre os campos eletromagnéticos e o meio de propagação.

As relações constitutivas descrevem como os campos elétricos e magnéticos interagem com a matéria.

Os meios podem ser compostos por moléculas que possuem propriedades elétricas e magnéticas, no qual possuem relações diretas com a propragação da energia eletromagnética.

Caso o meio for o vácuo, a composição atômica de sua formação é inexistente.

Essas relações são determinadas por 2 propriedades intrínsecas da matéria. São elas: Permeabilidade magnética e a permissividade elétrica.

Tais propriedades são grandezas de proporcionalidade que formam algebricamente as relações constitutivas do meio.

A Permeabilidade Magnética e a Permissividade Elétrica são a base para o entendimento das relações constitutivas de um meio material ou não. São elas:

Deslocamento Elétrico;
Densidade de Corrente;
Indução Magnética;

Estes últimos 3 tópicos descrevem as relações constitutivas de um meio.

2. Em Meios Lineares, Isotrópicos e Homogêneos

Os meios lineares, isotrópicos e homogêneos são conceitos fundamentais no estudo do eletromagnetismo e de outras áreas da física, relacionados com a forma como os materiais interagem com campos elétricos e magnéticos. Vamos detalhar cada um desses termos:

a. Meios Lineares

Um meio é considerado linear se a sua resposta aos campos elétricos ou magnéticos é proporcional à intensidade desses campos. Isso significa que as propriedades do material não mudam com a variação da intensidade do campo aplicado. Em termos matemáticos, se dobrarmos a intensidade do campo elétrico, por exemplo, a polarização (ou a densidade de fluxo elétrico) no material também dobrará.

Nas relações constitutivas, isso se traduz em:

$D = εE$ para o campo elétrico, onde $D$ é a densidade de fluxo elétrico, $ε$ é a permissividade do material, e $E$ é o campo elétrico.
$B = μ H$ para o campo magnético, onde $B$ é o campo magnético, $μ$ é a permeabilidade do material, e $H$ é o campo magnético auxiliar.

b. Meios Isotrópicos

Um meio é isotrópico se suas propriedades são as mesmas em todas as direções. Isso significa que a resposta de um material a um campo elétrico ou magnético não depende da direção desse campo. Por exemplo, se aplicarmos um campo elétrico em diferentes direções em um material isotrópico, a polarização induzida será a mesma em todas as direções.

A isotropia implica que as constantes $ε$ e $μ$ são escalares e não tensores, pois não variam com a direção do campo aplicado.

c. Meios Homogêneos

Um meio é homogêneo se suas propriedades são as mesmas em todos os pontos. Isso significa que a composição e a estrutura do material não variam no espaço. Em um meio homogêneo, a resposta a um campo elétrico ou magnético será a mesma, independentemente de onde o campo é aplicado dentro do material.

Quando um meio é ao mesmo tempo linear, isotrópico e homogêneo, as equações que descrevem o comportamento dos campos elétricos e magnéticos tornam-se mais simples e diretas, permitindo análises e cálculos mais fáceis em várias aplicações práticas, como na engenharia elétrica e na física de materiais.

3. Grandezas de Proporcionalidades:

a) Permeabilidade Magnética:

É a facilidade com que um material (ou meio material) tem para estabelecer um campo magnético.

É uma propriedade do material;
Representada matematicamente por $\mu$
Capacidade do material responder à presença de um campo magnético;
Capacidade do material ser magnetizado ou não;
Sua “resposta” significa que as estruturas elétricas internas do material se magnetizarem ou não;

\boxed{\vec{b} = \mu * \vec{h}}

As grandezas e unidades são:

indução  magnética  \rightarrow  [ \vec{b} ] = [T] \rightarrow Tesla

Permeabilidade  magnética  \to \boxed{[\mu] = \frac{[H]}{[m]}} \to Henry  por  metro

Campo  Magnético  \to  \boxed{[h] =\frac{A}{m}} \to Ampère  por  metro

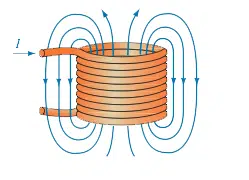
Valor da permeabilidade magnética no vácuo (meio não material):

$\boxed{\mu_0 = 4\pi*10^7 \frac{H}{m}}$

Valor de permeabilidade magnética em qualquer outro meio:

$\boxed{\mu= \mu_r * \mu_0}$

onde:

\mu_r \to Permeabilidade  relativa  do  meio

b) Permissividade Elétrica do Meio:

Imagine uma esponja de banho…Agora imagina que você despeje água nela de modo que ela fique “estufada”.

Nesse sentido, em algum momento essa esponja não consiguirá absorver mais água pois ela conquistou seu estado de saturação.

Disso, a capacidade de absorção de água na esponja chegou ao seu limite.

De forma analógica, permissividade elétrica é uma propriedade do meio que quantifica a capacidade do material (ou ausência dele) de armazenar cargas elétricas até que chegue no estado de saturação.

A fórmula que descreve o deslocamento elétrico d com a grandeza da permissividade elétrica está logo em baixo.

$\boxed{\vec{d} = \epsilon * \vec{e} }$

As grandezas e unidades são:

deslocamento  elétrico  \rightarrow  [ \vec{d} ] = [c]/[m^2] \rightarrow coulumb  por  metro  quadrado

Permessividade   elétrica  \to \boxed{[\epsilon] = \frac{[F]}{[m]}} \to Faraday  por  metro

campo  elétrico  \to  \boxed{[e] =\frac{V}{m}} \to volts  por  metro

A permissividade elétrica no vácuo é dada por:

$\boxed{ \epsilon_0 = 8,85*10^{-12} F/m}$

A permissividade elétrica em qualquer outro meio é dada por:

$\boxed{\epsilon = \epsilon_r * \epsilon_0}$

c) Condutividade Elétrica:

Capacidade do deslocamento ordenado de cargas (corrente elétrica de condução) quando submetidos a um campo elétrico.
Propriedade do meio material de locomover cargas elétricas quando submetidos à um campo elétrico.
A grandeza condutividade elétrica está correlacionado com a densidade de corrente elétrica (quantidade de corrente em ampères por unidade de área (m²)

Portando definimos que a densidade de corrente de condução é dada por :

$\boxed{\large{\vec{j} = \sigma * \vec{e }}}$

Onde:

\sigma \to condutividade  elétrica  [S]/[m] \to Siemens  por  metro

e  \to campo   elétrico  [V]/[m]

j \to densidade  de  corrente  elétrica  \to [A]/[m^2]

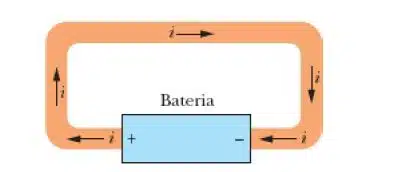
Portanto, fica como conclusão que as relações constitutivas são caracterizadas entre grandezas constantes e eletromagnéticas de modo que podemos determinar o deslocamento elétrico, a densidade de corrente de condução e indução magnética a partir das formulas acima que compõe as equações constitutivas do eletromagnetismo.

4. Exercícios:

Exercício 1: Campo Elétrico em um Capacitor

Problema: Um capacitor plano é feito de um material dielétrico linear, isotrópico e homogêneo, com permissividade relativa $\epsilon_r$ Se a densidade do fluxo elétrico entre as placas é de $E = \frac{D}{\varepsilon} = \frac{2.0 \times 10^{-3}}{3.54 \times 10^{-11}} \approx 56507 \, \text{V/m}$
, qual é a magnitude do campo elétrico no dielétrico?

Solução:

A relação constitutiva em um meio linear é $\mu = \mu_0 \mu_r = (4\pi \times 10^{-7}) \times 1000 \approx 1.256 \times 10^{-3} \, \text{Tm/A}$

E = \frac{D}{\varepsilon} = \frac{2.0 \times 10^{-3}}{3.54 \times 10^{-11}} \approx 56507 \, \text{V/m}

Significado: O campo elétrico de aproximadamente $56507 V/m$ representa a força elétrica por unidade de carga que atua dentro do material dielétrico. Este valor é uma consequência direta da densidade de fluxo elétrico aplicada e das propriedades do material.

Exercício 2: Magnetização em um Material Ferromagnético

Problema: Um material ferromagnético linear, isotrópico e homogêneo, com permeabilidade relativa $\mu_r = 1000$ e H = 200 A/m. Calcule a magnetização M do material.

Solução:

A relação constitutiva para campos magnéticos é $\mu = \mu_0 \mu_r = (4\pi \times 10^{-7}) \times 1000 \approx 1.256 \times 10^{-3} \, \text{Tm/A}$

Cálculo do campo magnético $B$ :

B = \mu H = (1.256 \times 10^{-3}) \times 200 \approx 0.2512 \, \text{T}

Cálculo da Magnetização do material:

M = \frac{B}{\mu_0} – H = \frac{0.2512}{4\pi \times 10^{-7}} – 200 \approx 795775 \, \text{A/m}

Significado: A magnetização de aproximadamente $795775 A/m$ indica a intensidade do momento magnético induzido no material por unidade de volume. Este valor alto é típico de materiais ferromagnéticos e mostra a forte resposta magnética do material ao campo aplicado.

Estes exercícios ilustram como as propriedades dos materiais lineares, isotrópicos e homogêneos influenciam a relação entre os campos elétricos e magnéticos e as quantidades físicas medidas, como o campo elétrico e a magnetização.

Conteúdos Recomendados:

Youtube: Professor Walter – UFSC

Livros recomendados:

Eletromagnetismo by John D. Krauss
RIBEIRO, José Antônio Justino. Propagação das ondas eletromagnéticas: princípios e aplicações
Eletromagnetismo – Willian Hayt and John Buck
Elementos do eletromagnetismo – Sadiku

Livros para construção Base da Teoria Eletromagnética:

Eletromagnetismo – Halliday – Volume III
Young & Freedman – Volume III
Eletromagnetismo (vol. 3), Volume 3. By Herch Moysés Nussenzveig