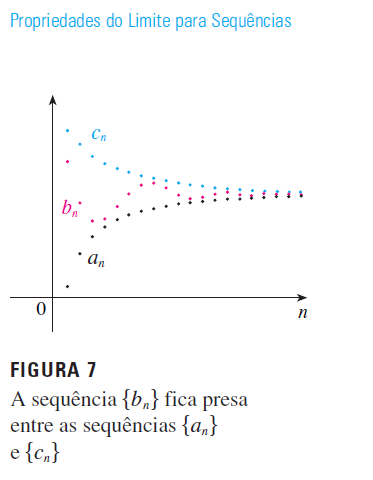
Sequências - Convergência e Divergência
1. Convergência ou Divergência de uma Sequência:
Vamos considerar que uma sequência possui infinitos elementos, ou seja, essa sequência vai de n=1 até , o valor de an, para n tendendo ao infinito irá definir se o mesmo será convergente ou divergente.
Para isso, vamos utilizar o conceito de limites, para definir o que logo segue:
Definição 1:
Uma sequência {an} é convergente, se o limite de n tendendo ao infinito da fórmula geral an for igual a um valor real L.
Ou seja, caso o limite denotado abaixo existir, dizemos que essa sequência é infinita.
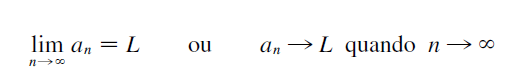
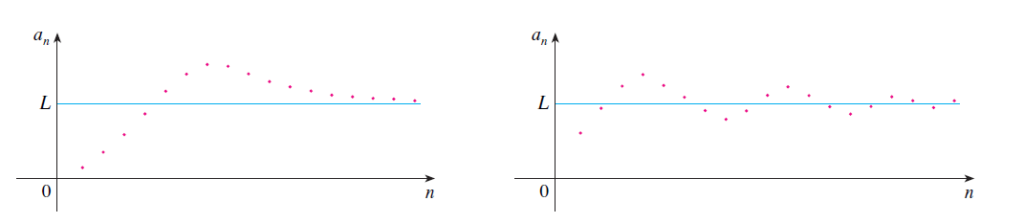
Caso contrário, esse limite dará valores não reais, como infinito positivo ou negativo. Então essa sequência é divergente.
Para todo n pertencente ao conjunto dos números inteiros, as propriedades de uma sequência são iguais das funções, assim visto em cálculo I. A partir dessa colocação, podemos descrever o seguinte teorema:
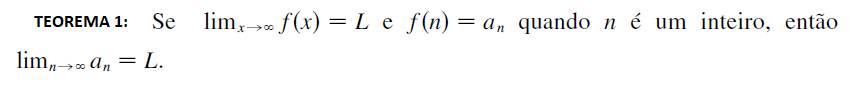
EXEMPLOS RESOLVIDOS:


EXERCÍCIOS PROPOSTOS - DIVERGÊNCIA E CONVERGÊNCIA DE SEQUÊNCIAS
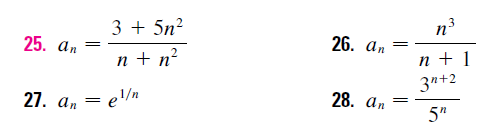
Um caso particular, seria a função f(x) = 1/xn , uma vez que consideramos n um número inteiro, então podemos fazer uma pequena mudança da notação de função para uma formula geral de sequência para um limite:
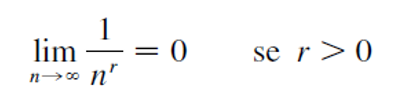
Utilizando o limite de uma sequência, temos disponíveis em nossas mãos, todas as ferramentas algébricas de limites, por tanto temos: