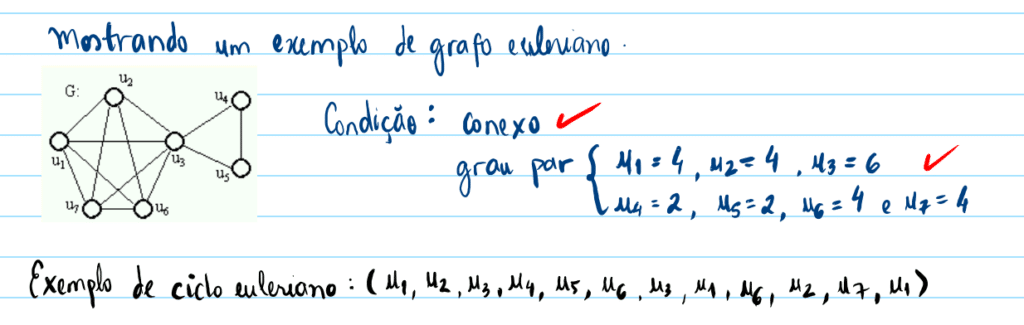Visto que vimos a definição de grafos, agora vamos discutir sobre o caminho que percorremos pelos vértices e aresta.

Inicialmente discutimos na primeira aula, sobre um dos primeiros contatos com a teoria dos grafos. Visto então que séculos atrás, o problema da mobilidade entre regiões de um cidade chamada Königsberg subdivida por portes. 

Um caminho Euleriano é um caminho em um grafo no qual visita todas as arestas exatamente uma vez.

Um Circuito Euleriano é um caminho euleriano que começa e termina no mesmo vértice. Um grafo com circuito euleriano é chamado de grafo euleriano.

Condição para o grafo ser Euleriano: O grafo deve ser conexo e o grau de todos os seu vértices serem iguais.

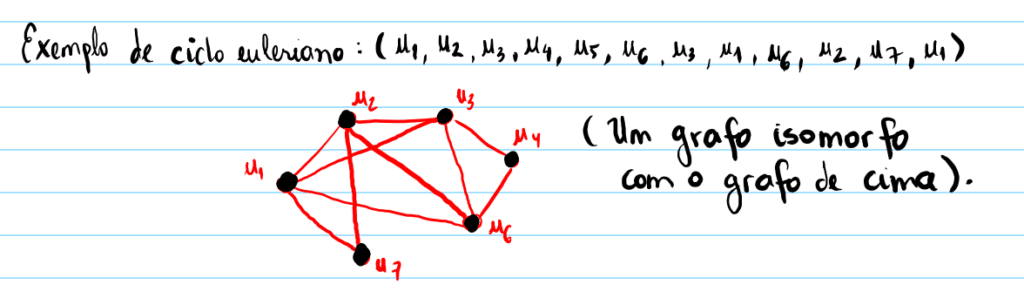
Um grafo G é dito ser euleriano se há um ciclo em G que contenha todas as suas arestas. Este ciclo é dito ser um ciclo euleriano. O grafo da figura ao lado, por exemplo, é euleriano já que ele contém o ciclo: (u₁, u₂, u₃, u₄, u₅, u₃, u₁, u₆, u₂, u₇, u_3, u₆, u₇, u₁), que é euleriano.

O teorema que se segue provê um solução simples para determinar se um grafo é euleriano:

Teorema: Um multigrafo M é euleriano se e somente se M é conexo e cada vértice de M tem grau par.

Agora, considere um multigrafo G tenha uma trilha (não um ciclo) contendo todas as arestas de M. Então G é dito ser um grafo atravessável e a trilha é dita ser uma trilha euleriana. No grafo ao lado, a trilha: (u₁, u₂, u₃, u₄, u₁, u₃, u₅) é atravessável.

O teorema seguinte indica precisamente quais grafos são atravessáveis:

Teorema: Um multigrafo M é atravessável se e somente se M é conexo e tem exatamente dois vértices de grau impar. Consequentemente, qualquer trilha euleriana de M começa em um dos vértices de grau impar e termina no outro vértice de grau impar.

EXEMPLOS: