Derivadas de Funções Trigonométricas
Nesta apostila, exploraremos as derivadas de funções trigonométricas, um tópico fundamental em cálculo diferencial. A compreensão dessas derivadas é crucial para estudantes de matemática, física, engenharia e outras áreas que utilizam cálculo em suas aplicações.
Introdução às Funções Trigonométricas e Derivadas
Antes de mergulharmos nas derivadas específicas, vamos revisar brevemente as funções trigonométricas básicas: seno (sin), cosseno (cos) e tangente (tan). Essas funções desempenham um papel vital no estudo de triângulos, ondas e muitos outros fenômenos naturais e técnicos.
As principais funções trigonométricas são o seno, cosseno, tangente, cossecante, secante e cotangente.
Calculando derivadas de Funções Trigonométricas a partir da Definição
Utilizando a definição formal de derivadas, vamos calcular as derivadas mais básicas como sen(x) e cos(x).
f'(x) = \lim_{h \to 0} \frac{f(x+h) – f(x)}{h}
Derivada do Seno
\frac{d}{dx} (\sin x) = \lim_{h \to 0} \frac{\sin(x + h) – \sin(x)}{h} \\[2em] \lim_{h \to 0} \frac{2 \sin(\frac{h}{2}) \cos(x + \frac{h}{2})}{h} \\[2em] \lim_{h \to 0} \frac{\sin(\frac{h}{2})}{\frac{h}{2}} \cos(x + \frac{h}{2}) \\[2em] \boxed{\frac{d}{dx}(sin(x)) = \cos x}
Derivada do Cosseno
\frac{d}{dx} (\cos x) = \lim_{h \to 0} \frac{\cos(x + h) – \cos(x)}{h} \\[2em] \lim_{h \to 0} \frac{-2 \sin(\frac{h}{2}) \sin(x + \frac{h}{2})}{h} \\[2em] \lim_{h \to 0} \frac{-\sin(\frac{h}{2})}{\frac{h}{2}} \sin(x + \frac{h}{2}) \\[2em] \boxed{ \frac{d}{dx}(cos(x)) = -\sin x}
Calculando a derivada da função Tangente a partir do Seno e Cosseno
Relembremos que:
tan(x) = \frac{sen(x)}{cos(x)}
Para derivarmos uma divisão de funções temos que utilizar a regra do quosciente.
\frac{d}{dx} (\tan x) = \frac{d}{dx} \left( \frac{\sin x}{\cos x} \right)\\[2em] \frac{d}{dx} (\tan x) =\frac{\cos x \cdot \frac{d}{dx}(\sin x) – \sin x \cdot \frac{d}{dx}(\cos x)}{\cos^2 x}\\[2em] \frac{d}{dx} (\tan x) = \frac{\cos x \cdot \cos x – \sin x \cdot (-\sin x)}{\cos^2 x}\\[2em] \frac{d}{dx} (\tan x) = \frac{\cos^2 x + \sin^2 x}{\cos^2 x}\\[2em] \frac{d}{dx} (\tan x) = \frac{1}{\cos^2 x}\\[2em] \boxed{\frac{d}{dx}(tan(x)) = \sec^2 x }
Derivadas de funções Trigonométricas: Um estudo Geométrico
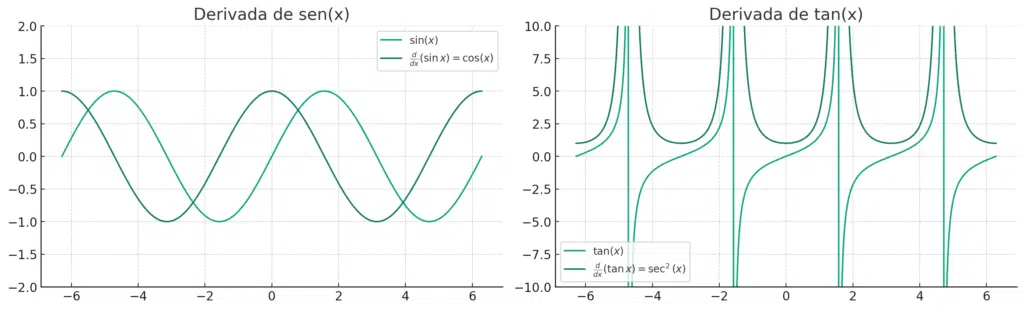
Derivar uma função trigonométrica, ou qualquer função, significa encontrar sua taxa de variação instantânea em cada ponto. Geometricamente, a derivada de uma função em um ponto específico é a inclinação da tangente à curva da função nesse ponto. Analiticamente, a derivada é a expressão que quantifica essa taxa de variação.
Nos gráficos que plotamos, a função inicial é representada pela linha contínua e a sua derivada pela linha tracejada. Observando o gráfico da função seno (sin(𝑥)sin(x)) e sua derivada, o cosseno (cos(𝑥)cos(x)), você pode ver que os picos e vales de sin(𝑥)sin(x) correspondem aos pontos onde a derivada cos(𝑥)cos(x) cruza o eixo x, indicando que a inclinação da tangente à curva sin(𝑥)sin(x) é zero nesses pontos – ou seja, a função original tem um ponto de máximo ou mínimo local.
No gráfico da função tangente (tan(𝑥)tan(x)) e sua derivada, a secante ao quadrado (sec²(𝑥)), as assíntotas verticais da tan(x) (onde a função tende ao infinito) coincidem com os picos de sec²(x).
Isso ocorre porque, à medida que a inclinação da tangente à curva tan(x) se torna mais íngreme, o valor de sec²(x) aumenta, refletindo a maior taxa de variação da função tangente próximo desses pontos.
Do ponto de vista crítico, é essencial que os alunos reconheçam as seguintes questões:
Geométrica: A derivada como a inclinação da linha tangente nos diz como a função está se movendo em cada ponto. Um valor positivo indica aumento, um valor negativo indica diminuição, e um valor zero indica um ponto onde a função pode ter um máximo ou mínimo local.
Analítica: A expressão da derivada nos dá uma fórmula para calcular essa taxa de variação para qualquer valor de x. É uma ferramenta poderosa para entender e prever o comportamento da função.
Crítica: É importante lembrar que nem todas as funções têm derivadas em todos os pontos. Por exemplo, a função tangente e sua derivada têm assíntotas onde elas não são definidas. Além disso, a simples existência de uma derivada não garante a continuidade da função original. O estudo das derivadas deve ser feito com uma compreensão das condições de existência e continuidade das funções.
Ao trabalhar com derivadas, os alunos devem se familiarizar com essas noções e praticar não apenas a mecânica do cálculo, mas também a interpretação e significado desses conceitos matemáticos.