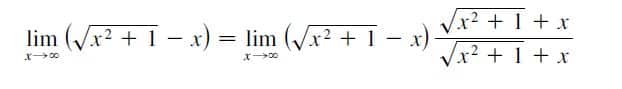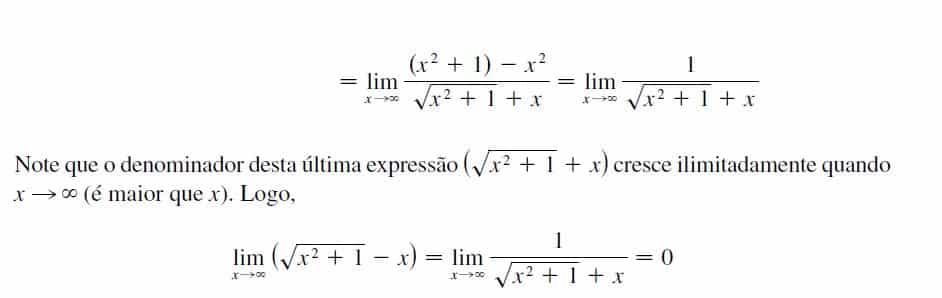Nessa aula vamos aprender o que são limites quando x tende ao infinito e negativo positivo, que serão representadas graficamente por suas curvas e assintotas horizontais.
Vamos ver que inúmeras funções podem tender a um valor L quando x é suficientemente grande.
Como pequena revisão vamos entender a diferença de assíntotas verticais e horizontais:
Como vimos na aula de assíntotas verticais, quando temos um valor de x tendendo a “a” e f(x) tende ao infinito positivo ou negativo, temos uma assintota vertical em x = a. Vejamos:
Assim, como já visto, temos algebricamente que:
\boxed{lim_{x \to a}{f(x)} = +\infty}
E sua assíntota:
\boxed{x = a}
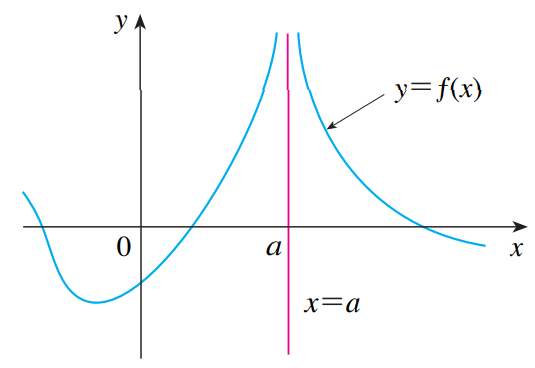
Já quando estamos falando de assíntotas horizontais, estamos nos referindo a retas horizontais, ou seja valores fixos para y mas muitos valores para x, sendo que y = f(x).
Ou seja uma assíntota vertical y = L, é uma reta no qual “delimita” o valor de um limite no qual x cresce suficientemente até o infinito. Para ficar mais claro vamos ver o exemplo de uma função.
Podemos denotar algebricamente o limite no infinito da seguinte forma (veja a diferença com o limite acima):
\boxed{lim_{x \to +\infty}{f(x)} = L}
Exemplo 1: Estude a função f(x) = \Large{\frac{x^2 – 1}{x^2 + 1}}
Para estudarmos esse tipo de função, vamos calcular os valores de f(x) para diferentes valores de x. No qual conseguimos chegar na seguinte tabela de valores:
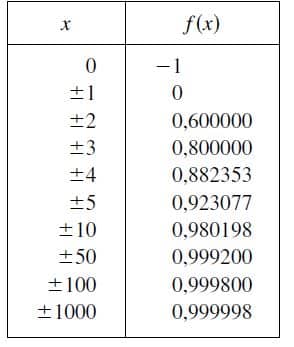
Veja que quanto maior o valor de x, f(x) se aproxima mais de 1. No final das contas percebemos que f(x) \to 1, quando x \to \pm \infty
Representando a função graficamente temos:
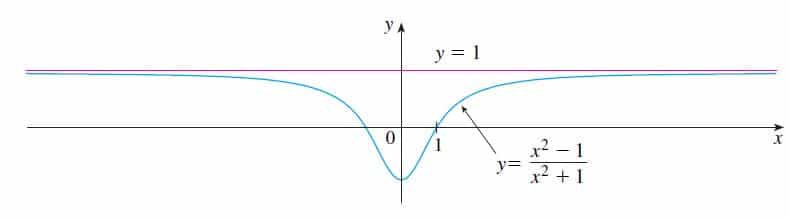
Falando de forma mais bonita, dizemos que nesse caso:
“Podemos deixar os valores de f(x) arbitrariamente próximos de 1 a medida que deixamos os valores de x suficientemente grandes”
Ou seja, conclui-se que:
\boxed{lim_{x \to \pm\infty}\frac{x^2 – 1}{x^2 + 1} = 1}
Definição 1:
Seja f uma função definida de (a,∞). Então:
\boxed{lim_{x \to \infty}{f(x)} = L}
Os valores de f(x) ficam arbitrariamente próximos de L, a medida que o valor de x cresce.
Podemos dizer da seguinte maneira:

Os valores da função podem se aproximar de L, de maneiras diferentes. observe os gráficos abaixo:
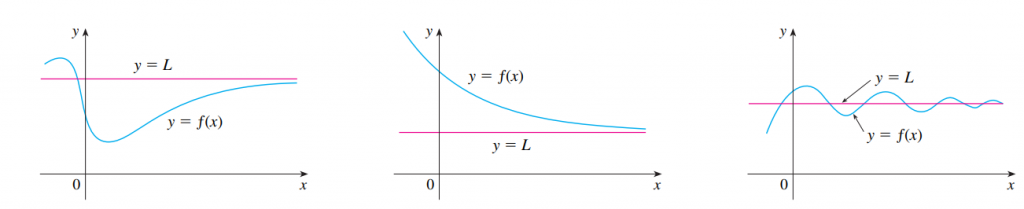
Gráfico 2: A função se aproxima por cima para o valor L.
Gráfico 3: Uma função oscilatória de que se aproxima de y=L.
Podemos também definir o limite de uma função que cresce ilimitadamente mas de forma negativa, ou seja x tende a menos infinito x \to – \infty, no gráfico do primeiro exemplo, la em cima, podemos ver que quando x \to – \infty, y = 1
Definição 2:
Seja f definida (-∞,a), temos que:
\boxed{lim_{x \to -\infty}{f(x)} = L}
A medida que o valor de x cresce ilimitadamente mas forma negativa, o valor de f(x) vai se tornando suficientemente perto de L.
Importante: Observe todos os gráficos, e neles há uma linha horizontal tal que y=L. Essas linhas retas e horizontais, de y=L, são chamados de Assíntotas Horizontais.
A condição algébrica para que y=L seja uma assíntota horizontal é dado pelos limites abaixo (ou seja, um desses limites devem ser satisfeitos):
\boxed{lim_{x \to +\infty}{f(x)} = L}
\boxed{lim_{x \to -\infty}{f(x)} = L}
Resolvendo Exercícios de Limites com Álgebra:
Lembre-se que muitos limites podem dar indeterminação!
Portanto vou listar algumas ideias que você tem que ficar em mente quando estiver resolvendo um limite com algebra:
Há uma soma de fração no limite? Faça M.M.C e Simplifique a função;
Há raiz quadrada no limite? Multiplique emcima e embaixo pelo seu conjugado e se possível, simplique a função.
Há uma divisão de Polinomios no limite? Busque fatorar as funções buscando o cancelamento de algum termo, simplificando a função.
Há funções senos e cossenos? Veja a possibilidade de utilizar o teorema do confronto.
Exercicios Resolvidos para Estudo:
Exercício 1) Encontre os limites infinitos e suas assíntotas horizontais e verticais de acordo com o gráfico abaixo.
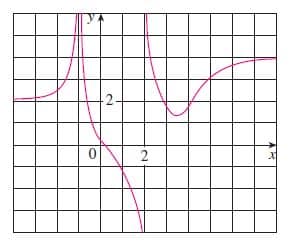
Vejamos que há muitos valores crescendo para todos os lados!!
De acordo com o gráfico acima:
Para x tendendo ao infinito negativo:
\boxed{lim_{x \to -\infty}{ y} = 2}
Para x tendendo ao infinito positivo:
\boxed{lim_{x \to +\infty}{ y} = 4}
Quando x tende a -1:
\boxed{lim_{x \to -1}{ y} = +\infty}
Quando x tende a 2:
\boxed{lim_{x \to 2}{ (y)} = +\infty}
Assíntotas Horizontais: \boxed{x = -1} \boxed{x = 2}
Assíntotas Verticais: \boxed{y = 2} \boxed{y = 4}
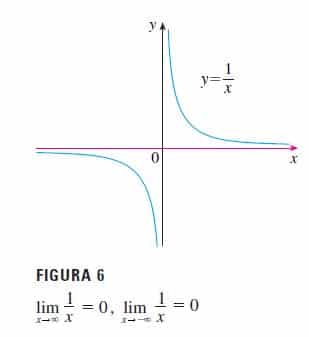
Exemplo 2: Encontre o lim_{x \to -\infty}{\Large{\frac{1}{x}}} e lim_{x \to +\infty}{\Large{\frac{1}{x}}}
Vamos fazer uma análise preliminar:
Considerando a função: f(x) = \Large{\frac{1}{x}}, vemos que enquanto maior o valor de x, menor o valor de f(x). Isso porque:
f(10) = \large{\frac{1}{10}} = 0,1
f(100) = \large{\frac{1}{100}} = 0,01
f(1000) = \large{\frac{1}{1000}} = 0,001
f(10000) = \large{\frac{1}{10000}} = 0,0001
A medida que x cresce, f(x) diminui! Portanto se x for uma valor gigantesco, em outras palavras. se x \to \pm \infty, então f(x) = 0!
Conclui-se que:
\boxed{lim_{x \to -\infty}{\Large{\frac{1}{x}}} = 0} \boxed{lim_{x \to +\infty}{\Large{\frac{1}{x}}} = 0}
Exemplo 3) Calcule lim_{x \to \infty}{\Large{\frac{3x^2 – x – 2}{5x^2 + 4x + 1}}}
Inicialmente vamos fazer a substituição direta. No entanto realizando ela acontece que:
lim_{x \to \infty}{\Large{\frac{3x^2 – x – 2}{5x^2 + 4x + 1} = \frac{\infty}{\infty}}}
Ou seja: Uma indeterminação!
Já que deu ruim em cima, vamos ter que utilizar manipulação algebrica para resolver esses tipos de exercícios.
Vamos fatorar a polinômio de cima e o polinômio de baixo, de modo que temos que “tirar” o x de maior ordem da fração. Vejamos:
lim_{x \to \infty}{\Large{\frac{x^2*(3 – 1/x – 2/x^2)}{x^2*(5 + 4/x + 1/x^2)}}} \to lim_{x \to \infty}{\Large{\frac{\cancel{x^2}*(3 – 1/x – 2/x^2)}{\cancel{x^2}*(5 + 4/x + 1/x^2)}}} \to lim_{x \to \infty}{\Large{\frac{(3 – 1/x – 2/x^2)}{(5 + 4/x + 1/x^2)}}}
Desse modo, sabemos que qualquer valor real dividido por infinito é zero! Assim:
\Large{\frac{(3 – \overbrace{1/\infty}^{0} – \overbrace{2/\infty^2}^{0})}{(5 + \overbrace{4/\infty}^{0} + \overbrace{1/\infty^2}^{0})}} = \Large{\frac{3}{5}} \to \therefore \boxed{lim_{x \to \infty}{\frac{3x^2 – x – 2}{5x^2 + 4x + 1}} = \frac{3}{5}}
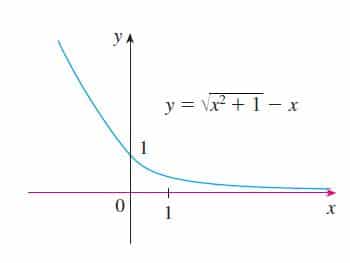
Exemplo 4) lim_{x \to \infty}{\large{\sqrt{x^2 + 1} – x}}
Novamente, vamos tentar pela substituição direta, o que nos ocasionará em uma situação de indeterminação!
Portanto, vamos realizar uma manipulação algebrica para determinar como simplificaremos nossa expressão. Quando temos raízes em uma indeterminação podemos multiplicar “em cima” e “em baixo” pelo o seu conjugado. Vejamos: