Arcos e Circunferências
Parte 1:
Definição:
Inicialmente consideramos dois pontos A e B em uma circunferência C:
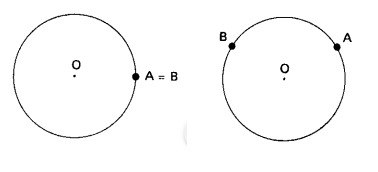
Com dois pontos distintos, a circunferência possui duas partes, cada uma das partes – que é esse espaço entre A e B – são chamadas de arcos de circunferência.
Se A e B se coincidirem, como na circunferência da esquerda, um dos arcos AB = 0 e o outro arco AB = 1 volta completa.
Medidas de arcos:
Antes de tudo, para conseguirmos fazer medições de arcos devemos adotar uma medida. Para isso, dividimos a circunferência em partes iguais e definimos um valor para cada parte.
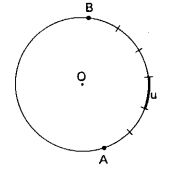
Unidades mais utilizadas:

Portanto conclui-se que um volta inteira da circunferência foi dividida em 360 partes iguais, cada parte equivale a 1 grau.
Outra unidade muito utilizada é o radianos (rad), durante os estudos da circunferência, foi definido que um volta completa equivale a 6,2835…rad batizado então de 2π rad. Podemos dizer que radiano é o arco unitário cujo o comprimento é igual ao raio da circunferência que o contêm.
Portanto já adiantando que 360º = 2π rad = 1 volta completa.
Submúltiplos do grau:
i) Minuto: 1/60 do grau – simbolo: ( )’
ii) Segundo: 1/60 do minuto – simbolo: ( )”
Se um arco AB tem 20 graus, 20 minutos e 10 segundos, representamos dessa forma: AB=20°20’10”
Transformação de unidades:
Será muito comum e necessário transformar da unidade grau para radianos e de radiano para grau. Para a transformação destes, basta fazer um regra de 3, tal que:
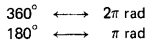
Medidas e ângulos:
Agora que sabemos as principais unidades utilizadas no cálculo de arcos de circunferência e sabemos transforma-los, vamos ver as medidas dos arcos:
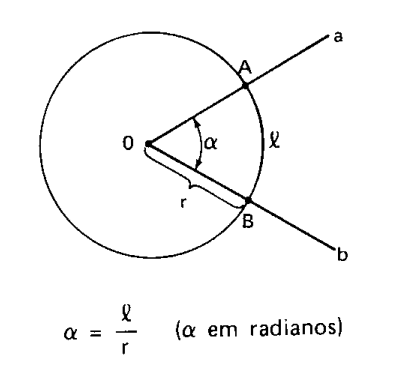
- L= medida do arco AB.
- r = raio da circunferência
- α = ângulo AÔB, dado em radianos
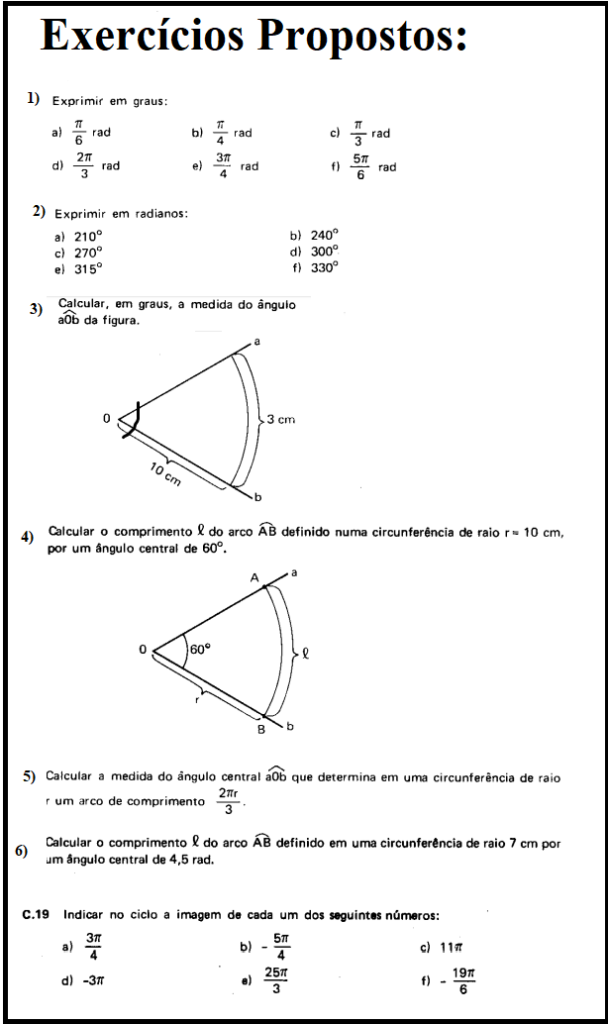
Agora é sua vez! Faça esses exercícios, caso não conseguir não tem problema! Veja o gabarito. Nessa aula temos repertório suficiente para fazer os exercícios 1 até 6.