O divergente de uma função vetorial tem uma enorme importância no mundo do cálculo vetorial, para acadêmicos e aqueles que amam a ciência exata, digo que é elementar aprender o que é um divergente e como funciona suas aplicações.
O que é Divergente de uma Função Vetorial?
É um operador matemático aplicado à funções vetoriais. O resultado da divergente descreve a taxa com que um campo vetorial está se “aproximando” ou está se “afastando” de um determinado ponto.
Essa operação é muito utilizado em conceitos de fluxo vetorial (Lei de Gauss) no qual desenvolve-se nas teorias eletromagnéticas e da mecânica dos fluídos, também podemos estender seu conceito para a dispersão de comportamentos de funções vetoriais que representam uma gama da natureza biofísica e bioquímica.
Definindo o Divergente de uma Função Vetorial:
Seja uma função vetorial de classe C¹, ou seja, suas derivadas parciais de primeira ordem existem em dado domínio B, definida como:
\vec{F} = P \hat{i} + Q \hat{j} + R \hat{k} P, Q e R são funções escalares no qual ditam a função vetorial F como é o comportamente vetorial nas componentes unitárias de x, y e z.
A divergente de uma função vetorial é dada por:
div{F} = \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} + \frac{\partial R}{\partial z}
Ou seja calculando, as derivadas parciais de cada componente e somando-os.
Veja que a derivada parcial em x está relacionado com a função P, onde tem direção em i, a derivada parcial em y com Q que está relacionado com seu vetor unitário j, e a derivada parcial em z está relacionado com a função correspondente ao vetor unitário na direção z, que no caso é k.
Divergente de uma função Vetorial a partir de Produto Escalar:
Imagine uma certa região do espaço. Por exemplo, pegue um ponto, desenhe um quadrado ou um circulo ou qualquer outra figura sendo ela pontual, bidimensional ou tridimensional. A divergente nos diz que:
\vec{\nabla}.\vec{F} > 0 Se o divergente for positivo, a somatória dos vetores (haverão mais vetores se afastando do que se aproximando dessa determinada região do espaço).
Chamamos esse ponto de Fonte.
\vec{\nabla}.\vec{F} < 0 Se o divergente for negativo, a somatória dos vetores (haverão mais vetores se aproximando do que se afastando dessa determinada região do espaço).
Chamamos esse ponto de Sorvedouro.
Seja o operador nabla em forma vetorial:
\vec{\nabla} = \frac{\partial}{\partial x}\hat{i} + \frac{\partial}{\partial y}\hat{j} + \frac{\partial}{\partial z}\hat{k}Vamos aplicar um produto escalar entre o nabla definido acima e F definido no primeiro tópico:
\vec{\nabla}.\vec{F} = \left(\frac{\partial}{\partial x}\hat{i} + \frac{\partial}{\partial y}\hat{j} + \frac{\partial}{\partial z}\hat{k}\right). (P \hat{i} + Q \hat{j} + R \hat{k})\therefore \vec{\nabla}.\vec{F} = \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} + \frac{\partial R}{\partial z}Que é a mesma definição da acima, então podemos introduzir a divergente de F como uma notação de um produto escalar entre um vetor nabla e o campo vetorial F.
Interpretação Geométrica da Divergente de um Campo Vetorial:
Veja o gráfico de uma função vetorial dada por:
\vec{F} = x^2\hat{i} + y^2\hat{j}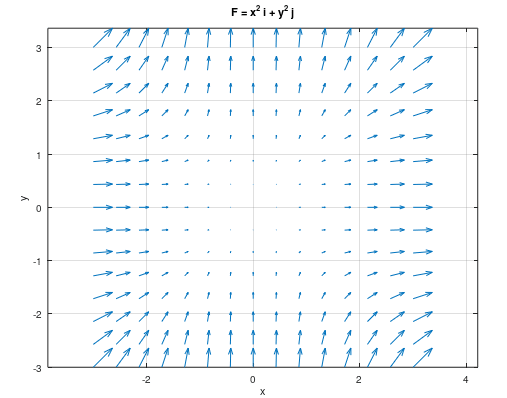
A cada ponto P(x,y) há uma seta que representa um vetor, ou seja tem módulo, direção e sentido. A divergente da função a cima é dada por:
div\vec{F} = \frac{\partial F_x}{\partial x} + \frac{\partial F_y}{\partial y} = \frac{\partial }{\partial x}(x^2) + \frac{\partial }{\partial y}(y^2) = 2x + 2y Vamos definir agora para que valores de x e y que o divergente é positivo ou negativo.
Assim, podemos ver em que pontos do espaço vetorial a função possui um fluxo geral de afastamento ou aproximação.
div\vec{F} = 0 \to 2x + 2y > 0 \therefore \boxed{y > -x}Vejamos que se traçarmos uma reta y = – x, vamos obter um divegente positivo em pontos na diagonal superior, e um divergente negativo na diagonal inferior.
Isso significa que todos os ponto em que y > -x, qualquer ponto do espaço terá divergente positiva.
Portanto terão maior fluxo vetorial de afastamento do que de aproximação. Esses pontos são chamados de Fonte.
No caso contrário, o divergente é negativo.
Assim, temos um fluxo vetorial maior de aproximação do que de afastamento.
Esses pontos serão chamados de Sorvedouro.
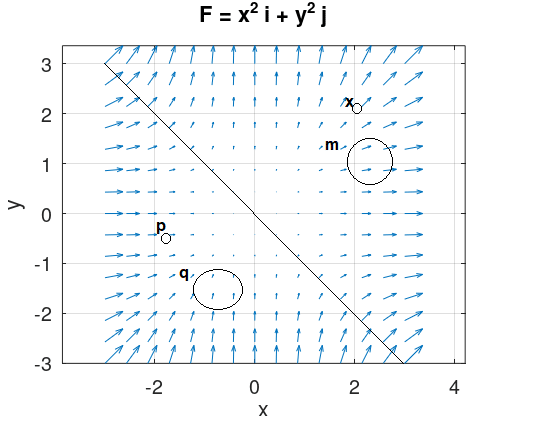
Veja a figura abaixo, abaixo da linha y = – x, temos p e q, no qual as setas entram muito mais do que saem, no quesito de magnitude total, por isso possuem divergente negativo, já em x e m as setas saem muito mais em magntude, o que nos traz a tona um divergente positivo.
No próximo post resolveremos muitos exercícios sobre esse conceito.
Não perca a chance de resolve-los.
Entenda melhor esses conceitos para construir base totalmente sólida na teoria das exatas!
Um grande abraço,
Eric.




