Menu
A continuidade da corrente elétrica baseia-se na lei da conservação de energia. Vamos mostrar que a corrente elétrica de condução e de deslocamento devem sempre seguir essa lei.
O exemplo abaixo é um circuito simples: Um capacitor e uma fonte de tensão alternada. Nele vamos determinar como a corrente elétrica de condução se relaciona com a corrente elétrica de deslocamento de modo a obedecer a lei de conservação de carga.
Exercício 1) Mostre a continuidade da corrente elétrica no circuito abaixo:
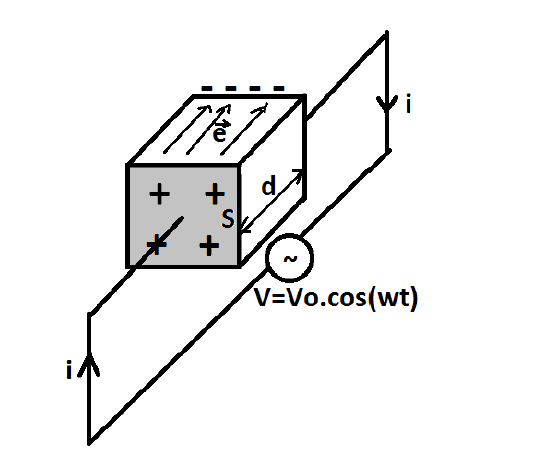
Devemos definir os dois tipos de correntes elétricas e depois compara-las.
A corrente de condução é o movimento ‘real’ das cargas elétricas e é dado pela lei de Ohm:
(1) I = \frac{V}{R}
Calculamos a corrente de condução como a quantidade de cargas elétricas que atravessam em uma secção transversal em um determinado tempo. Algebricamente expressamos como a variação da carga elétrica no tempo.
(2) i_c = \frac{dQ}{dt}
A capacitância é um propriedade dos capacitores onde mensura a capacidade do armazenamento de cargas elétricas sobre determinada tensão. Explicito abaixo:
C = \frac{Q}{V}
Portanto sabemos que a carga elétrica no capacitor é dada por:
Q(t) = V(t).C
A tensão dada no exercício é V = V_o.cos(\omega t)
Desse modo, temos que:
Q(t) = – C.V_o.cos(\omega t)
Colocando isso na eq. 2, calculamos a corrente de condução:
i_c = \frac{dQ(t)}{dt} = \frac{d}{dt}(C.V_o.cos(\omega t)
\boxed{i_c = -C.\omega.V_o.sen(\omega t)}
A corrente de deslocamento trata-se da variação do campo elétrico. De acordo com as leis de Maxwell, a variação do campo elétrico gera uma corrente de deslocamento. Descrito da seguinte forma:
\mathbf{J}_d = \epsilon_0 \frac{\partial \mathbf{E}}{\partial t}
Para tal cálculo, precisamos saber o que é a densidade de corrente de deslocamento dado por:
j_d = \frac{i_d}{S}Onde:
S é a área da secção transversal do capacitor;
i_d é a corrente de deslocamento;
Em outras palavras a densidade de corrente de deslocamento é a quantidade de corrente de deslocamento por determinada quantidade de área (A/m²)
Desse modo:
i_d = S. j_di_d = S. \epsilon_0 \frac{\partial \mathbf{E}}{\partial t}