Inicialmente devemos refletir o motivo pelo que novas teorias e novas definições da matemática são desenvolvidas. Mais especificamente em Cálculo I estudamos as integrais, e elas são operações sob um eixo unidimensional ou seja de uma dimensão. As integrais simples foram definidas primitivamente para determinar áreas sobre curvas.
No Cálculo III as integrais múltiplas são operações que agem em uma função de 2 ou 3 variáveis dado por f(x,y) ou f(x,y,z).
No caso das integrais duplas, elas operam acima de um plano Oxy do ℜ2 em uma função de duas variáveis f(x,y), veremos que esses tipos de operações possuem a capacidade de determinar volume de um sólido do ℜ3.
De acordo com a Geometria Espacial aprendemos a calcular volumes de muitas figuras tridimensionais, grande parte delas partem do produto entre a área da base e a altura. V = Ab. H
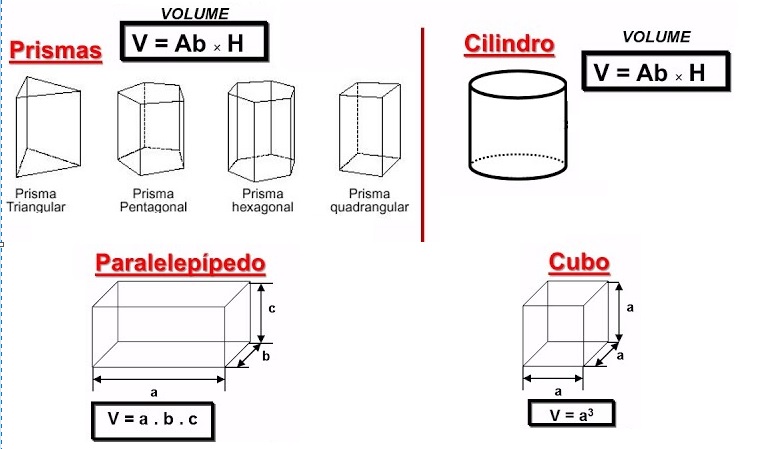
Porém essas figuras são regulares – o que deixa muito mais fácil de determinar o seu volume – Agora imagine a seguinte situação: Calcular o volume do sólido descrito na figura abaixo.
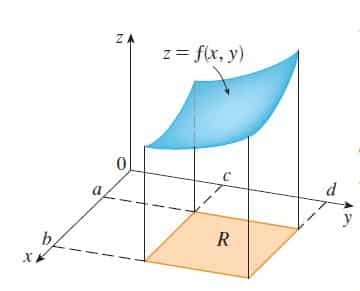
Uma figura como essa não é regular pode ser baseada em uma função de x e y tal que z = f(x,y). Para determinarmos qual é esse volume não é tão simples como as figuras regulares antes dito. É aí que entra as integrais duplas, uma operação utilizada para calcular o volume de sólidos irregulares em que sua altura se comporta como funções de duas variáveis.
Para definirmos uma integral dupla, vamos tentar calcular a integral em que seu domínio é um retângulo. Vamos partir da formula básica: V = Ab.h assim como propões a geometria analítica.
Considerando uma função de duas variáveis f(x,y) e também definida em um retângulo.
Definimos esse Retângulo da seguinte forma: R = [a,b] x [c,d] { (x,y) ∈ ℜ2/ a ≤ x ≤ b, c ≤ y ≤ d }.
Portanto o domínio retângular é dado por:
\boxed{ R = \{[a,b] * [c,d] { (x,y) ∈ ℜ^2/ a ≤ x ≤ b, c ≤ y ≤ d }. \}}
Nesse retângulo vamos dividi-los em vários sub-retângulos, ou seja, dividiremos no eixo ox o intervalo de [a,b] em m subintervalos de mesmo comprimento [xi-1, xi], o mesmo vale para o eixo oy, no qual dividiremos o intervalo [c,d] em n subintervalos de mesmo comprimento [yj-1, yj]. Veja a figura abaixo:
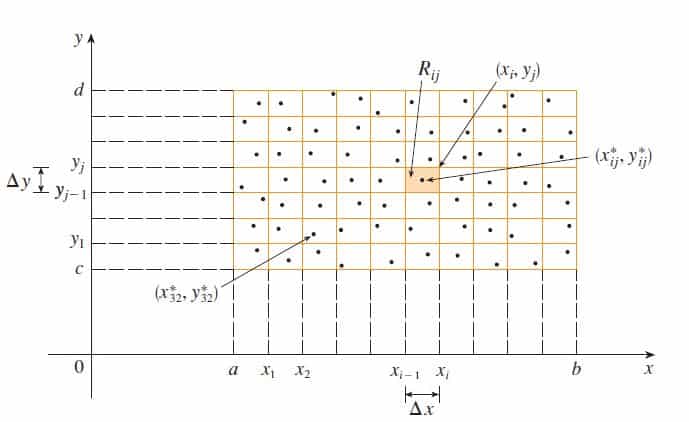
Essa divisões dos intervalos [a,b] em m subintervalos e [c,d] para n subintervalos são chamados de partições. E a partir dessas partições são gerados m.n sub-retângulos cada sub-retângulo é definido da seguinte forma:
\boxed{ R = \{R_{ij}= [x_{i-1}, x_i] * [y_{j-1}, y_j] | { x_{i-1} ≤ x ≤ x_{i} , y_{j-1} ≤ y ≤ y_{j} } \}}
A área do Retângulo inicial é dado por A = b.h e no caso A = (b – a).(d – c). No caso de cada sub-retângulo sua base é expressa por Δx e sua altura por Δy. Portanto a área de Rij
\therefore \Delta A = \Delta x * \Delta y
Onde geometricamente (Analise o gráfico), temos que:
\boxed{\Delta x = \large{\frac{b-a}{m}}}
\boxed{\Delta y = \large{\frac{d-c}{n}}}
Inicialmente devemos refletir o motivo pelo que novas teorias e novas definições da matemática são desenvolvidas. Mais especificamente em Cálculo I estudamos as integrais, e elas são operações sob um eixo unidimensional ou seja de uma dimensão. As integrais simples foram definidas primitivamente para determinar áreas sobre curvas.
No Cálculo III as integrais múltiplas são operações que agem em uma função de 2 ou 3 variáveis dado por f(x,y) ou f(x,y,z).
No caso das integrais duplas, elas operam acima de um plano Oxy do ℜ2 em uma função de duas variáveis f(x,y), veremos que esses tipos de operações possuem a capacidade de determinar volume de um sólido do ℜ3.
De acordo com a Geometria Espacial aprendemos a calcular volumes de muitas figuras tridimensionais, grande parte delas partem do produto entre a área da base e a altura. V = Ab. H
Considerando a figura abaixo:
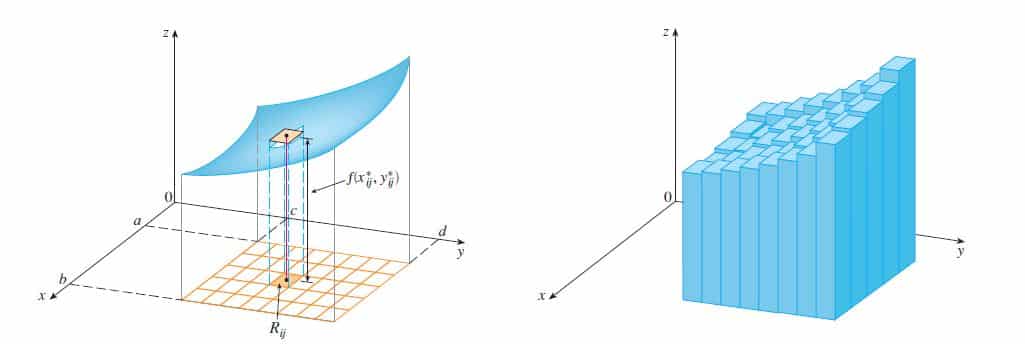
Se o volume é dado por V = Ab.h, a área da base pode ser considerado pelo retângulo R que pertence ao plano Oxy, e sua altura é o valor de z = f(x,y). A integral dupla vem do conceito da somatória de um número muito grande de sub-volumes vindo do produto de ΔA.f(x,y) – que é o volume de cada caixa subdividida – Portanto:
\boxed{\Large{V = \sum\limits_{i=1}^{n} \sum\limits_{j=1}^{m} f(x_i,y_j) \Delta A}}
Essa equação é chamada de Somatória Dupla de Riemannn, usada então como base para a Definição de integrais.
Enquanto maior o número de divisões, ou seja, maior o número de sub-retângulos, menor será o erro entre o volume calculado e o volume real do sólido. Logo se pudermos deixar o número de sub-divisões tão grande quanto quisermos podemos, o valor dessa somatória será igual ao valor do volume real do sólido. Para tal conceito os valores de m e n devem tender ao infinito.
m \to \infty e n \to \inftyAssim chegamos então na seguinte formula:
\boxed{\Large{V = \lim_{m,n \to \infty}{\sum\limits_{i=1}^{n} \sum\limits_{j=1}^{m} f(x_i,y_j) \Delta A}}}
Se esse limite existir, a integral dupla de f sobre o retângulo R é dupla somatório infinita de Riemann do produto de f(x,y) com a área daquele subdivisão.
\boxed{\Large{\iint\limits_R f(x,y) \, dA = \lim_{m,n \to \infty}{\sum\limits_{i=1}^{n} \sum\limits_{j=1}^{m} f(x_i,y_j) \Delta A}}}
Se somente se, o limite existir!
Se acalma! É estranho entender desse jeito. Mas vamos com calma. No começo dessa aula subdividimos a base retângular em inúmeros quadrados minúsculos, e assim temos infinitos volumes com altura f(x,y) e base ΔA. O volume disso é o produto dos dois! E o volume total é a soma de tudo!!
Além disso, para todo f(x,y) ≥ 0, podemos afirmar que essa integral dupla é o Volume do sólido.
\boxed{ V = \iint\limits_R f(x,y) \, dA}
Linearidade:
\boxed{\iint\limits_R (af(x,y) + bg(x,y)) \, dA = a\iint\limits_R f(x,y) \, dA + b\iint\limits_R g(x,y) \, dA}
Aditividade:
\boxed{\iint\limits_{R_1 \cup R_2} f(x,y) \, dA = \iint\limits_{R_1} f(x,y) \, dA + \iint\limits_{R_2} f(x,y) \, dA}
Monotonicidade: Se f(x,y) ≤ g(x,y) em um retângulo R, então:
\boxed{\iint\limits_R f(x,y) \, dA ≤ \iint\limits_R g(x,y) \, dA}