Em cálculo, os limites laterais nos ajudam a entender o comportamento de uma função à medida que nos aproximamos de um ponto específico 𝑥=𝑎x=a pelo lado esquerdo (limite lateral esquerdo) ou pelo lado direito (limite lateral direito). Isso é particularmente útil quando a função não é definida exatamente em 𝑥=𝑎x=a ou se comporta de maneira diferente de cada lado desse ponto.
Limite Lateral Esquerdo: denotado como \lim_{x \to a^-} f(x) , refere-se ao valor para o qual f(x) se aproxima conforme x se aproxima de 𝑎a pelo lado esquerdo.
Limite Lateral Direito: denotado como \lim_{x \to a^-} f(x) , refere-se ao valor para o qual f(x) se aproxima conforme x se aproxima de 𝑎a pelo lado direito.
Usamos como exemplo, para introduzir o assunto de limites laterais, a função de Heaviside, H.
A função é definida como:
Quando estamos falando em limites, temos que estar atento em valores que tendem a um determinado número, mas não são efetivamente o próprio número.
Ou seja quando dizemos que:
x \rightarrow 0 , não significa que x é igual a 0 , mas que x tem um valor suficientemente próximo a 0 .

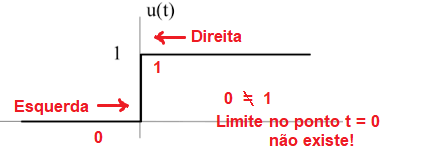
Observe que há dois caminhos para chegar no ponto t=0. Podemos aproximar o valor de t pela esquerda ou podemos aproximar pela direita.
Aproximação pela esquerda: São valores de t < a, e portanto seu intervalo de (t, a). Ex: aproximação pela esquerda para t=0, temos: (t=-0,5; -0,2; -0,1; -0,01; -0,001, …). Cada vez o valor de t chega mais perto de t=0, porém com t<0.
Aproximação pela direita: São valores de t>0 e portanto seu intervalo de (a, t). Ex: Aproximação pela direita para t=0, temos:(t= 0,5; 0,2; 0,1; 0,01 , …). cada vez o valor de t chega mais perto de 0, porém com valores de t>0.
Devemos concluir que: Limites podem tender ao mesmo valor, mas eles dependem do caminho de aproximação também. Observe que pode acontecer dos limites laterais terem valores diferentes e portanto o limite não existe!
Leia: Condição de existência de um limite.
Recurso Externo – Leitura Rápida: Limites Laterais e Condição de Existência de um Limite
Vou repetir e guarde isso com muito carinho: Se o valor de f(x) que se aproxima de um ponto pela esquerda ser diferente do valor de f(x) que se aproxima pela direita, o limite nesse determinado ponto não existe!
Formalizando o que escrevi logo em cima, escrevemos:
\lim_{x \to a^-} f(x) = L
“O limite à esquerda de f(x), quando x tende a a é igual a L.”
Podemos tornar f(x) = L , quando há valores de x suficientemente perto de a, se somente se x<a.
Da mesma forma temos que:
Escrevemos:
\lim_{x \to a^+} f(x) = L
“O limite à direita de f(x), quando x tende a a é igual a L.”
Podemos tornar f(x) = L, quando há valores de x suficientemente perto de a, se somente se x<a.
Formalizando o que escrevi logo em cima, escrevemos:
\lim_{x \to a^-} f(x) = L
“O limite à esquerda de f(x), quando x tende a a é igual a L.”
Podemos tornar f(x) = L , quando há valores de x suficientemente perto de a, se somente se x<a.
Da mesma forma temos que:
Escrevemos:
\lim_{x \to a^+} f(x) = L
“O limite à direita de f(x), quando x tende a a é igual a L.”
Podemos tornar f(x) = L, quando há valores de x suficientemente perto de a, se somente se x<a.
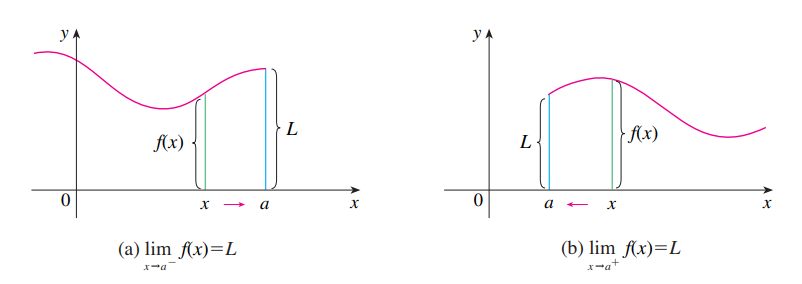
O limite de f(x), quando x tende a a só existirá, se somente se, os valores dos seus limites laterais forem iguais. Algebricamente expressamos da seguinte forma:
\lim_{x \to a} f(x) = L se, e somente se, \lim_{x \to a^-} f(x) = L e \lim_{x \to a^+} f(x) = L
Os limites laterais devem ser iguais!
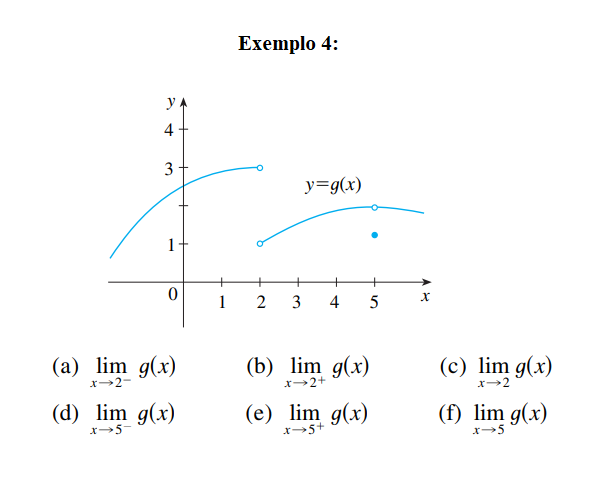
Analisando os gráfico e fazendo os caminhos dos valores temos:
a) \boxed{\lim_{x \to 2^-} g(x) = 3} “O limite de g(x) quando x tende pela esquerda de 2 é igual a 3”
b)\boxed{\lim_{x \to 2^+} g(x) = 1} “O limite de g(x) quando x tende pela direita de 2 é igual a 1”
c) Veja que pela definição 3, concluímos que o limite de x tendendo a 2 não existe. Pois:
\boxed{\lim_{x \to 2^+} g(x) = 1 \neq \lim_{x \to 2^-} g(x) = 3}
\boxed{lim_{x \to 2} g(x) = \not\exists}
d) \boxed{\lim_{x \to 5^+} g(x) = 2}
e) \boxed{\lim_{x \to 5^-} g(x) = 2}
f) \boxed{\lim_{x \to 5^+} g(x) = 2 = \lim_{x \to 5^-} g(x) = 2}, portanto \boxed{lim_{x \to 5} g(x) = 2}
Independente se g(5) = 1 !!! Estamos falando de valores no limite e não efetivamente de x = 5 !!