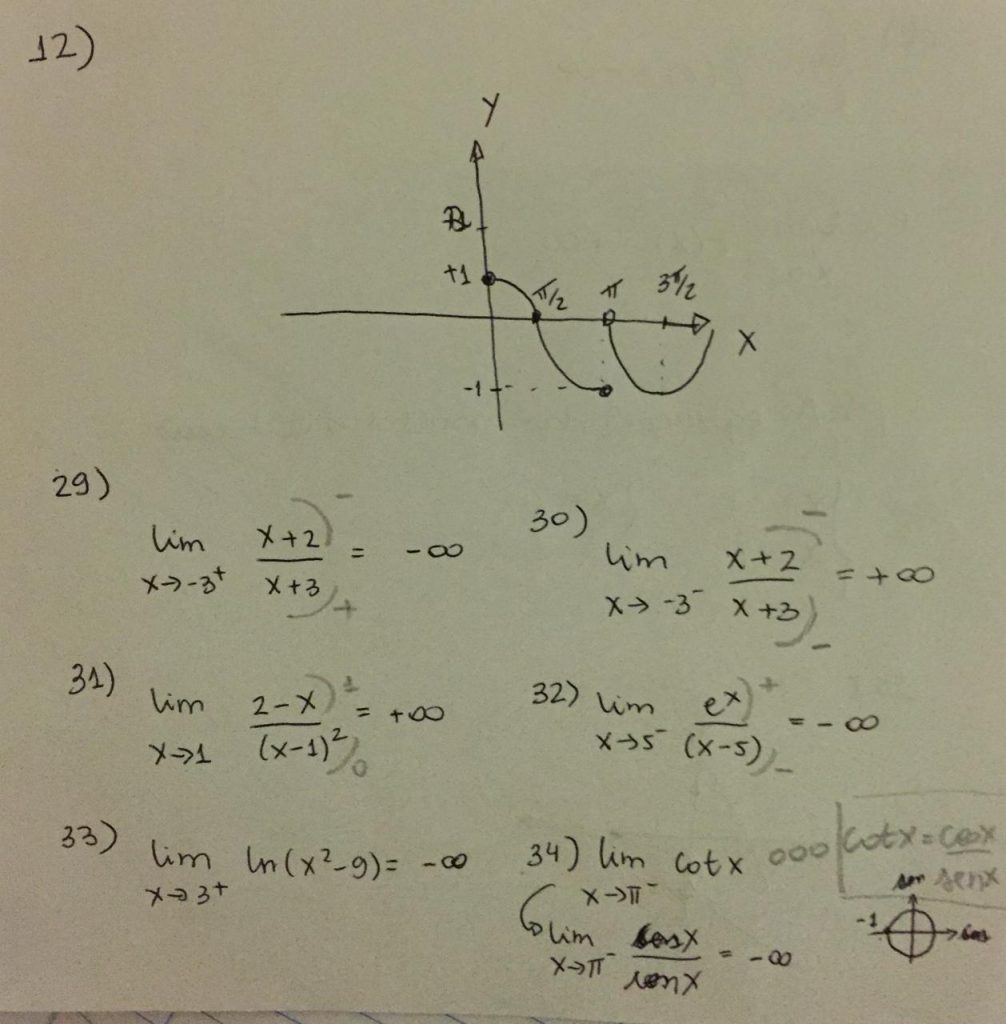
Resposta Exercício 5:
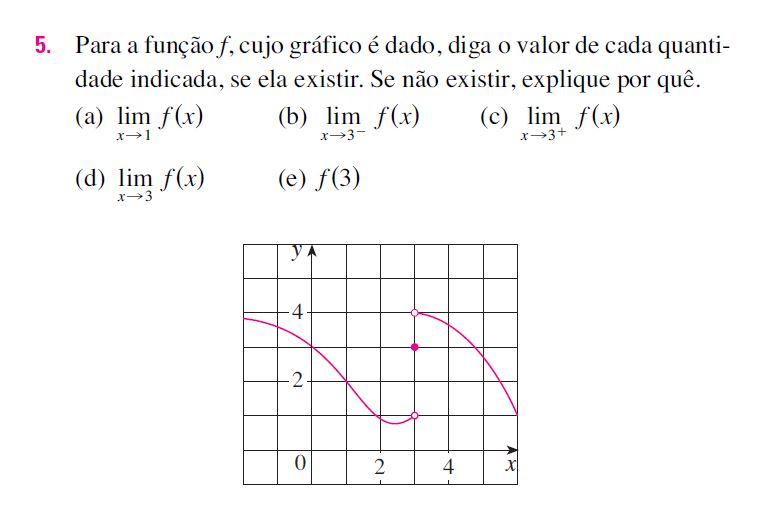
a) Como resposta podemos análisar o gráfico. Vemos que para x =1 e suas vizinhanças o
\boxed{ lim_{x \to 1}f(x) = 1}
para os exercícios b) c) d) e) temos que tomar muito cuidado. É necessário entender o que está acontecendo. Pois quando olhamos para vizinhança esquerda de x = 3; y = 1, quando olhamos a vizinhança direita de x = 3; y = 4 e quando olhamos exatamente no ponto x = 3, temos o ponto definido (pintado em bolinha escura) representado y = 3. Portando concluímos pelos valores dos limites:
b) Olhando então na vizinhança esquerda representamos o valor do limite vindo da esquerda:
\boxed{lim_{x \to 3^-}f(x) = 1}
c) Olhando então na vizinhança direita representamos o valor do limite vindo da direita:
\boxed{lim_{x \to 3^+}f(x) = 4}
d) Agora vejamos, que lim_{x \to 3}f(x) = não existe! pois seus limites laterais são diferentes! Portanto:
lim_{x \to 3^-}f(x) \neq lim_{x \to 3^+}f(x)
e) Já agora, por x estar definido no gráfico (bolinha escura), mesmo que o limite não exista, não quer dizer que f(x) não exista também!
Nesse caso f(3) existe. e \boxed{f(3) = 3}
Resposta Exercício 7:
Veja que o exercício 7 tem exatamente o mesmo raciciocínio. Fazemos juntos esse exercício e o próximo fica com vocês resolverem! Me mande email se estiver com dúvida.
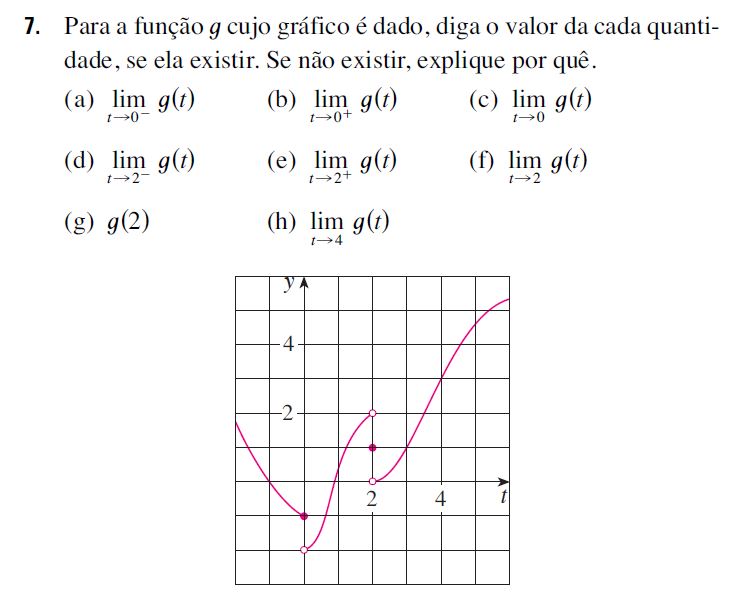
a) Vamos analizar a vizinhança esquerda da função g(t) com t = 0. De acordo com o gráfico:
\boxed{ lim_{t \to 0^-}g(t) = -1 }
b) Agora analizamos o lado direito da vizinhança em t = 0; Assim:
\boxed{ lim_{t \to 0^+}g(t) = -2 }
c) Olha que belezaaa! Esse limite existe? Claro que não! Vou ficar desapontado se me dizer que sim! E por que não?
Os limites laterais são diferentes! Não há continuidade!
Portando \boxed{ lim_{t \to 0}g(t) = não existe! }
Pois:
\boxed{ lim_{t \to 0^-}g(t) \neq lim_{t \to 0^+}g(t)}
d) Agora vamos estudar os limites e os valores na vizinhança de t = 2; Poranto, quando t tende pela esquerda de g(t) para t = 2, temos:
\boxed{ lim_{t \to 2^-}g(t) = 2}e) agora, estamos tendendo pela direita de t = 2, de acordo com o gráfico:
\boxed{ lim_{t \to 2^+}g(t) = 0 }f) E já sabemos que esse limite não existe, pois os limites laterias são diferentes. Portanto esse limite não existe.
\boxed{ lim_{t \to 2^-}g(t) \neq lim_{t \to 2^+}g(t)}g) Vemos que o ponto escuro no gráfico mostra que existe um g(t) definido em t = 2. Portanto:
g(2) = 1
h) O limite em t = 4 está continuamente definido, portanto temos que:
\boxed{ lim_{t \to 4}g(t) = 3}