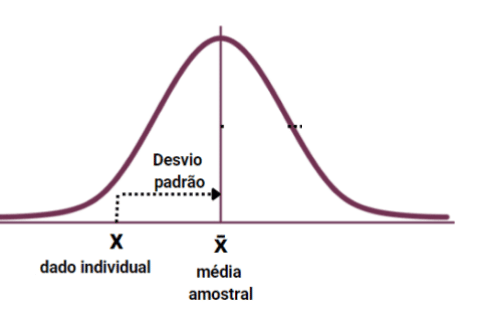
As medidas de dispersão são cálculos complementares à análise de dados.
Vimos já com uma forma de análise, vimos em Medidas Descritivas de Posição que podemos definir como um conjunto de dados é concentrado com o uso do cálculo da Média Aritmética por exemplo.
Esses cálculos são muito importantes para a análise estatística de um conjunto de observações. Por outro lado, seria ineficaz analisar a concentração de valores das observações se houver padrões não lineares e com muita variança e/ ou dispersões.
Em outras palavras, as medidas descritivas de posição oculta a informação de como esse gráfico varia e como os pontos se dispersam em relação a um referencial.
As medidas de dispersão nos fornece como os dados variam em relação as medidas de posição, por isso, essa relação de complementariedade entre a posição e a dispersão no comportamento dos dados.
São algumas Medidas de Dispersão: Amplitude, Variança, Desvio Padrão, Intervalo Interquartil e o Coeficiente de Variação.
O que você precisa saber para ler esse artigo:
Cálculo da Amplitude
Amplitude com Variáveis Discretas:
A amplitude de um conjunto de valores é dado pelo diferença entre o maior valor e o menor valor;
A = Q_{maior} - Q_{menor}Onde:
Q_ {maior} \to \text{É o maior valor do conjunto numérico} Q_ {menor} \to \text{É o menor valor do conjunto numérico}Considerando um grupo de alunos com as seguintes notas e suas médias, temos:
| Grupo de Alunos | Notas | Média | Amplitude Notas |
|---|---|---|---|
| A | 3,4,5,6,7 | 5 | 7 – 3 = 4 |
| B | 1,3,5,7,9 | 5 | 9 – 1 = 8 |
| C | 5,5,5,5,5 | 5 | 5 – 5 = 0 |
| D | 3,5,5,7 | 5 | 7 – 3 = 4 |
| E | 2,4,5,5,9 | 5 | 9 – 2 = 7 |
Amplitude com Variáveis Contínuas:
Quando as variáveis são contínuas o cálculo da amplitude torna-se diferente;
Devemos calcular o ponto médio dos salários e assim calcula-se a amplitude geral com o maior ponto médio menos o menor ponto médio.
A = PM_{maior} - PM_{menor}Onde:
PM_{maior} \to \text{Maior valor médio da coluna Salários}PM_{menor} \to \text{Menor valor médio da coluna Salários}| Classes | Salários | Ponto Médio | Frequência |
|---|---|---|---|
| 1 | 2├─ 4 | 3 | 5 |
| 2 | 4├─ 6 | 5 | 2 |
| 3 | 6 ├─ 8 | 7 | 20 |
| 4 | 8 ├─ 10 | 9 | 7 |
| 5 | 10 ├─ 12 | 11 | 2 |
A amplitude é dado portanto por A = 11 – 3 = 8
Desvio Médio Simples
Vejamos outro cálculo de variáveis de dispersão chamada de desvio médio simples.
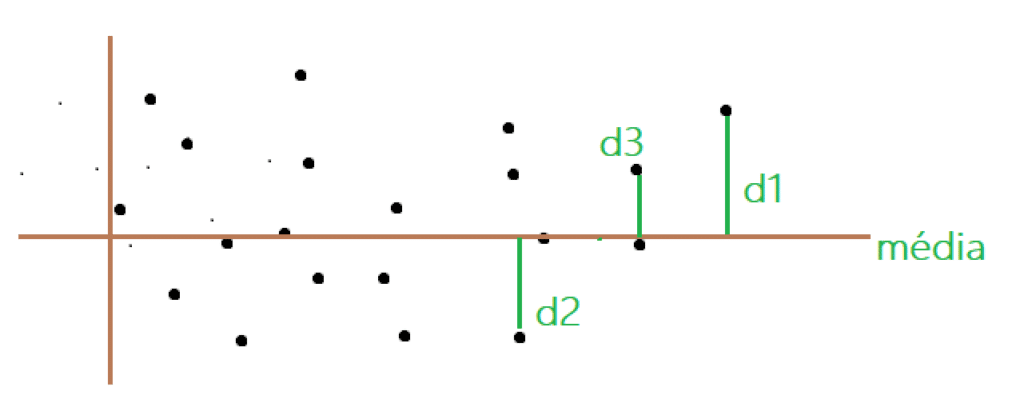
Imaginemos um gráfico com vários pontos com seus valores no qual a média aritmética também é traçada.
Vejamos que média pode representar uma linha de concentração dos pontos, porém não omite como os pontos variam em relação à média
O desvio médio representa o quanto os pontos variam em relação à média aritmética.
- Desvio médio com valores altos – representam maior dispersão dos pontos pretos representados e distâncias maiores da média;
- Devio médio com valores baixos – representam caminhos mais uniformes e mais próximos da média;
DMS = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (x_i - \bar{x})^2}
\sigma \text{ representa o desvio padrão.} \\
N \text{ é o número de observações no conjunto de dados.} \\
x_i \text{ são os valores individuais no conjunto de dados.}\\
\bar{x} \text{ é a média dos valores no conjunto de dados.}\\
x_i \text{ e a média } \bar{x} \text{ ao longo de todas as observações.}
Desvio médio Simples – Variável Discreta
Para variáveis discretas calculamos utilizando a seguinte fórmula:
DMS = \frac{1}{N} \sum_{i=1}^{N} |x_i - \bar{x}|
Considerando a frequência relativa fi temos:
DMS = \sum_{i=1}^{N} |x_i - \mu| \cdot f_i
\text{DMS representa o Desvio Médio Simples.} \\
\text{N é o número de observações no conjunto de dados discreto. }\\
x_i \text{ são os valores individuais no conjunto de dados.} \\
\bar{x} \text{ é a média dos valores no conjunto de dados.} \\
\\
Desvio médio Simples – Variável Continua
\sigma = \sqrt{\int (x - \mu)^2 \cdot f(x) \, dx}
Cálculos com Dispersão de Pontos em torno da Média:
Variança : Variáveis Discretas (Dispersão)
s^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2
s^2 \text{ representa a variância amostral.} \\ [10px]
n \text{ é o tamanho da amostra.}\\ [10px]
x_i \text{ são os valores individuais na amostra.} \\ [10px]
\bar{x} \text{ é a média dos valores na amostra.}
Variança: Variáveis Contínuas (Dispersão)
s^2 = \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2s^2 \text{ representa a variância amostral.} \\ [10px]
n \text{ é o tamanho da amostra.}\\ [10px]
x_i \text{ são os valores individuais na amostra.} \\ [10px]
\bar{x} \text{ é a média dos valores na amostra.}
Dispersão – Desvio Padrão: Variável Discreta
s = \sqrt{\frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2}
Dispersão – Desvio Padrão: Variável Contínua
s = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2}Coeficiente de Variança:
Coef = \left(\frac{s}{\bar{x}}\right).100\%Scores Z:
Z = \frac{x-\bar{x}}{s}