Problema da tangente e da velocidade

Introdução:

Na história da matemática, toda teoria proviam de problemas matemáticos que os recursos do conhecimento não eram suficientes para a sua resolução. O problema da tangente em curvas complexas, assim como outros fenômenos físicos como a velocidade se tornaram algo extremamente discutido entre os séculos XVII e XVIII, no qual o conceito de limites e derivadas se tornaram essênciais ferramentas para tais entendimentos.

Tangente a uma curva:

Uma tangente a curva é uma reta que toca somente uma vez em um certo ponto na curva. Para isso acontecer a reta deve ter a mesma direção que a curva em um ponto específico. Como exemplo, podemos citar uma reta tangenciando um círculo:

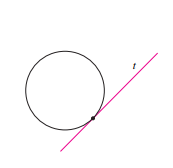
A reta t tangencia o círculo. Para Euclides no caso, a reta tangente de um círculo é aquela que intercepta o círculo em um único ponto. Porém o problema da tangente vem quando a reta intercepta curvas mais complexas.

O problema da tangente:

Observe a imagem abaixo, principalmente as retas que interceptam o círculo:

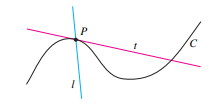
Da figura 2, temos duas retas que são t e l, e também uma curva mais complexa C. Observe que:

A reta t tangencia a curva C? Pela direção da reta t, aparentemente essa reta tangencia a curva porém observe que a reta t intercepta dois pontos da curva, o que contradiz os conceitos de Euclides.
A reta l tangencia a curva C? Diferente da reta t , a reta l intercepta apenas uma vez na curva, porém o Ângulo da reta não coincide com o ponto da curva, contradizendo novamente os conceitos de Euclides.

Exemplo 1) Encontre a equação da reta tangente à parábola y = x² no ponto P(1,1)

Fique em mente: A equação da reta é preciso de dois pontos onde é calculado pela fórmula: $y - y_o = m.(x - x_o)$

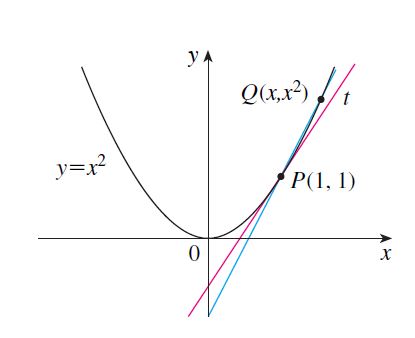
Primeiramente para encontrar uma reta tangente à parábola x² no ponto (1,1), dado pela figura 3, devemos conhecer a inclinação dessa reta. Dado por:

m = \frac{\Delta y}{\Delta x}

Vejamos que a equação 1 temos que:

m = \frac{y  –  y_o}{x  –  x_o}

Isto é, somente poderíamos calcular o coeficiente angular da reta (inclinação da reta) com no mínimo dois pontos $P_o (x_o, y_o) e P (x,y)$

Portanto, o grande problema da tangente torna-se quando precisamos de dois pontos para calcular uma equação da reta tangente, mas a tangente por outro lado por definição somente encosta em um ponto da curva. Uma grande contradição!

Estratégia: Vamos calcular diversas retas secantes(retas que passam por dois pontos PERTENCENTES à curva). Uma vez que queremos a tangente do ponto P(1,1), devemos escolher o ponto (1,1) e outro próximos a (1,1).

Mudando um pouco a formula da inclinação da reta dado em cima:

$m = \frac{y – y_o}{x – x_o} = \frac{x^2 – 1}{x – 1}$

Assim, vamos considerar alguns pontos que pertecem à curva e vamos calcular seu coeficiente ângular:

Já que y = x², podemos considerar que os pontos que pertencem à curva possuem a seguinte condição como: Q (x, x²); Ou seja para:

x = 1,5 temos y = (1,5)² = 2,25, agora sim conseguimos ter dois pontos no qual dois pontos $P_o (1,5; 2,25) e P (1,1)$

$m = \frac{2,25 – 1}{1,5 – 1} = 2,5$

Da mesma forma que fizemos emcima, podemos fazer com valores de x cada vez mais próximos de x =1. De modo a chegarmos da seguinte tabela de cálculos de coeficientes angulares:

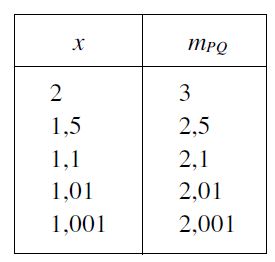
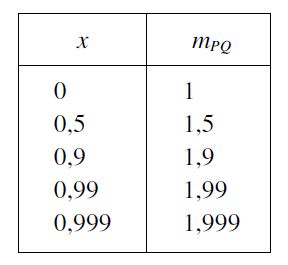
Por que estamos fazendo isso? Pois, no final das contas queremos um coeficiente angular que reflita somente no ponto P(1,1), então estamos aproximando o valor de x -> 1 até chegarmos em um valor de m exageradamente próximo do que queremos calcular!

E assim, reparamos que tanto quando x se aproxima por baixo, como x se aproxima por cima de 1, o valor de m se aproxima muito para m = 2. O que podemos concluir que o coeficiente ângular da reta tangente a curva no ponto (1,1) é 2!

Preste atenção na figura abaixo que a medida que o ponto Q se aproxima do ponto P, a reta vai ficando cada vez mais “tangente à curva no ponto”.

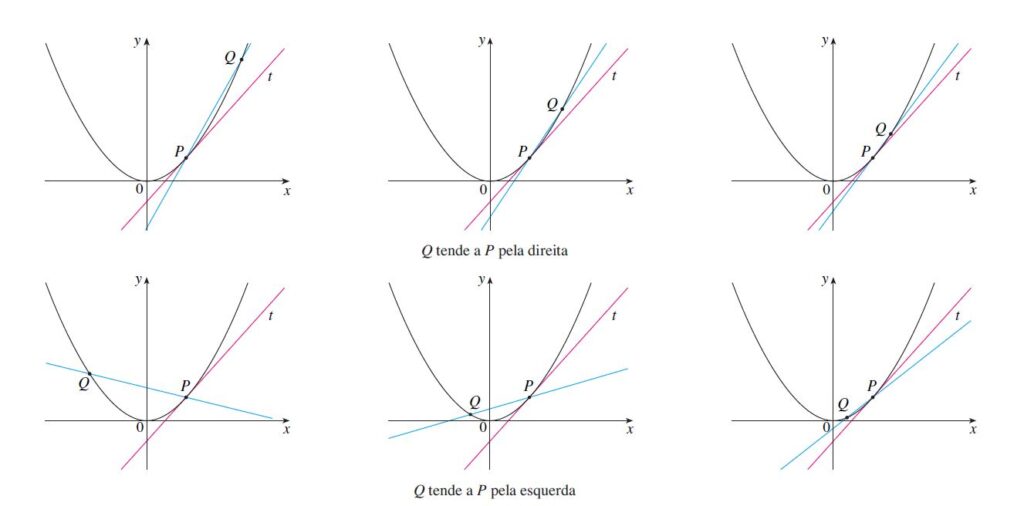
Quando um ponto se aproxima suficientemente de outro tornando-a uma tangente aquela curva, podemos falar em limite, no qual:

$\lim_{Q \to P} f(x) = 2$

Falamos em voz alta da seguinte maneira: “O limite de f(x) do ponto Q tendendo ao Ponto P é igual a 2”

Assim a equação da reta torna-se:

$y - y_o = m* (x - x_o)$

$y - 1 = 2*(x - 1)$

$y = 2x - 2 + 1$

$\boxed{ y = 2x -1 }$

E assim introduzimos mais que uma solução viável ao problema da tangente, mas também o conceito de limite que será extremamente importante para aprender cálculo e todos outros conteúdos de exatas!