Nesse capítulo vamos focar na resolução de triângulos que são não retângulos, portanto não há um ângulo de 90º no triângulo. Uma forma de calcular lados e ângulos desses triângulos é usando as leis do seno e cosseno.
Observe que um triângulo retângulo não possui nenhum ângulo obtuso, então se houver algum ângulo de 90º dentro desse triângulo, os outros ângulos necessariamente irão ser menores que 90º.
1) Seno e cosseno de ângulos obtusos:
Inicialmente precisamos saber que o sen(90º)= 1 e cos(90º)=0 .
Um ângulo obtuso é um ângulo que está entre (90º,180º). Então vou lhes mostrar um método que conseguimos calcular seno e cosseno de ângulos maiores que 90º e menores que 180º.
- Calculo de seno de ângulos obtusos: O seno dos ângulos obtusos são exatamente iguais ao seno de seus ângulos complementares, portanto:
senx = sen(180º-x)
- Calculo do cosseno de ângulos obtusos: Já o cosseno de ângulos obtusos são iguais ao negativo do cosseno de seus ângulos complementares, portanto:
cosx = – cos(180º-x)
Exemplos resolvidos:
- Calcule o seno e o cosseno dos seguintes ângulos:
a) sen(120º) e cos(120º)
b) sen(135º) e cos(135º)
c) sen(150º) e cos(150º)
RESOLUÇÃO:

2) Lei dos senos:
Considerando o triângulo ABC, a relação do seno de um ângulo é sempre proporcional à medida do lado oposto a esse ângulo.
A razão entre um lado e o seno do seu ângulo oposto é uma constante. Assim podemos igualar as razões dos lados e de seus ângulos opostos a uma razão R.
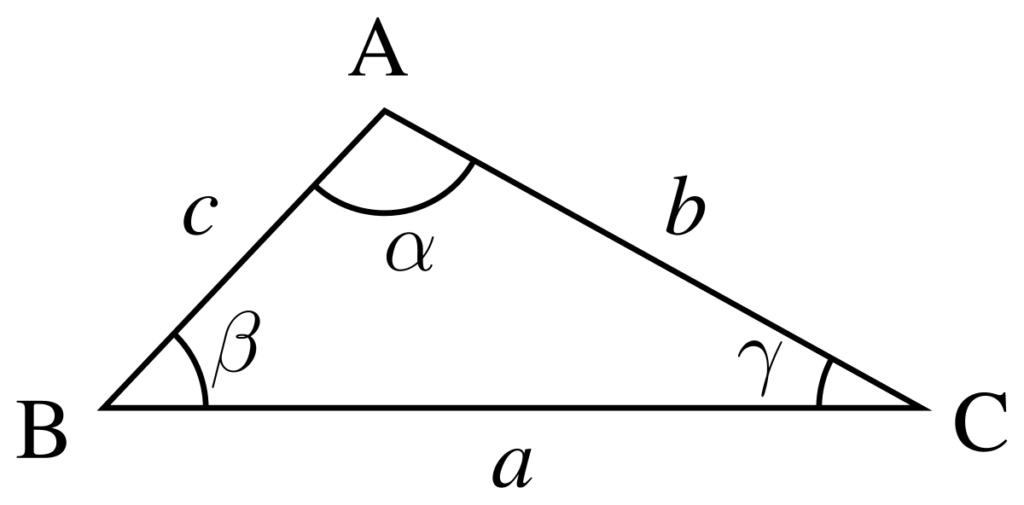
O teorema anuncia que:
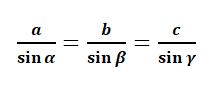
3) Lei dos cossenos:
Podemos usar esse teorema quando possuirmos a medida de dois lados e o ângulo oposto do terceiro lado. Assim, considerando o triângulo ABC, a lei dos cossenos anuncia que:
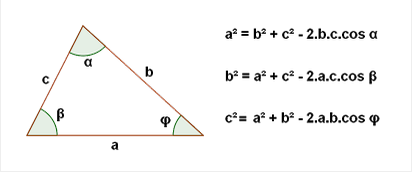
a2 = b2+c2 – 2bc(cos90) -> a2 = b2+c2 -> Sobra apenas o teorema de pitágoras!