Um triângulo retângulo é aquele que possui um angulo de 90º.

Existem definições que podem ser dadas em cada um dos lados do triângulo:
Importante destacar que o cateto oposto e o cateto adjacente são dependentes do ângulo em questão, que nesse caso é α (C)
hipotenusa = É o lado oposto ao ângulo de 90º (Â) no triângulo é BC ou a.
Cateto adjacente = é lado mais próximo do ângulo α que é o lado CA ou b.
Cateto oposto = é o lado oposto ao ângulo α que é o lado AB ou c.
Importante destacar que o cateto oposto e o cateto adjacente são dependentes do ângulo em questão, que nesse caso é α (C)
hipotenusa = É o lado oposto ao ângulo de 90º (Â) no triângulo é BC ou a.
Cateto adjacente = é lado mais próximo do ângulo α que é o lado CA ou b.
Cateto oposto = é o lado oposto ao ângulo α que é o lado AB ou c.
Definições dos valores de seno, cosseno e tangente:
Em questão das funções trigonométricas seno, cosseno e tangente fique tranquilo, nas próximas aulas você vai se aprofundar nelas. Por enquanto o importante é ver como essas funções se comportam no triângulo retângulo e quais são seus valores quando estão em ângulos notaveis.
Considerando o triângulo retângulo da figura 1:

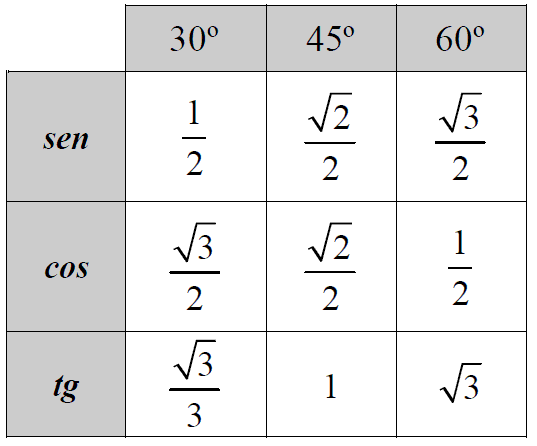
Valores do seno, cosseno e tangente de ângulos notáveis:
Os ângulos notáveis são 30º , 45º e 60º: