Conceito de Resposta em Frequência:
A resposta em frequência na eletrônica analógica mostra o comportamento do ganho de dispositivos eletrônicos em função da frequência.
A frequência angular é dada por radianos por segundos. [rad/s]
A representação gráfica da resposta em frequência é dada pelo diagrama de Bode. Nesse caso, podemos analisar diversos parâmetros que um circuito analógico possui.
Podemos projetar filtros, osciladores e amplificadores de um circuito analógico a partir do diagrama de bode.
Desde um circuito de amplificação de Som, como os mais complexos sistemas eletrônicos podem ser modelados a partir da análise da resposta em frequência em eletrônica analógica.
Resposta em Frequência: Largura de Banda
A largura de banda é a faixa de frequência que um amplificador opera.
Essa faixa de frequência tem uma operação que não é prejudicada pelas frequências dos capacitores ou por frequências dos componentes internos do amplificador.
Capacitores externos alteram a resposta em frequência em baixas frequências.
Capacitores internos alteram a resposta em frequência em altas frequências.
Representação da resposta em frequência: Diagrama de Bode
Representação gráfica da resposta em frequência de um amplificador e/ ou outro sistema.
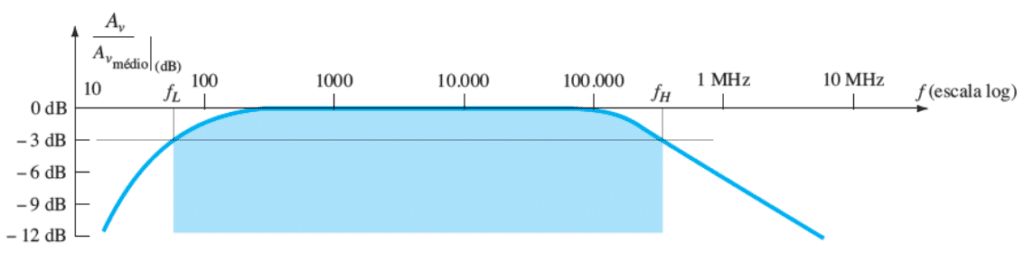
Vejamos que a figura acima, representa o diagrama de bode onde:
- Eixo x: Frequência em hertz (Escala Logaritmica)
- Eixo y: Temos o ganho que é dado na unidade dB (Decibéis)
Faixa de média frequência: Região do gráfico onde o ganho fica constante ou quase constante.
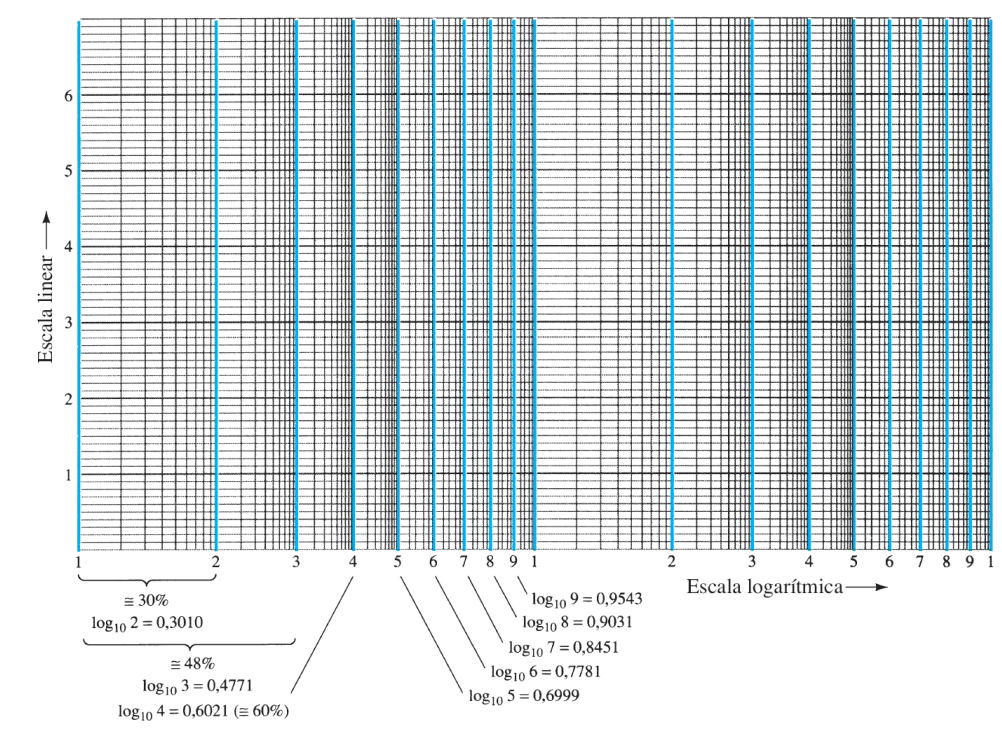
Eixo x da Resposta em Frequência: Escala Logaritma
Usamos os logarítmos na base 10.
Portanto temos:
x = log_{10}(a)Exemplo de uma escala:
Unidade em Decibeis:
- Relaciona o ganho em dB com a potência em Watts [W]
- Quando falamos em decibeis, estamos focando em ganho de potência de um sistema.
- Uma vez que na elétrica o ganho de potência é dada pela tensão. Podemos considerar dB como ganho de tensão (Terceira fórmula).
Consideremos a potência P_1 e P_2, temos a relação do ganho em função das potências da seguinte forma:
G = log\left(\frac{P_1}{P_2}\right) [bel]Quando temos 10 bels temos 1 decibel. Dessa maneira, transformamos a equação de cima como:
G = 10*log\left(\frac{P_1}{P_2}\right) [dB]Considerando um dispositivo eletrônico que possui uma resistência R, uma tensão inicial V_1 e V_2.
Podemos fazer a seguinte relação de ganho dada uma tensão:
G_{dB} = 20*log\left(\frac{V_1}{V_2}\right) [dB]Ganho em decibéis com dispositivos em Cascata:
O ganho quando se trata de seu valor absoluto pode ser obtido multiplicando cada um dos seus respectivos valores:
|A_{v}| = |A_{v1}| * |A_{v2}| * |A_{v3}| ...Quando esses ganhos estiverem na unidade decibeis, devemos somar esses ganhos:
G_v = G_{v1} + G_{v2} + G_{v3} + ... [dB]Exercício Resolvido:
Um amplificador com 40 W de saída é conectado a um auto-falante de 10 Ω.
a. Calcule a potência de entrada quando o ganho de potência é de 25 dB.
b. Calcule a tensão de entrada quando o ganho de tensão do amplificador é de 40 dB.
25 (dB) = 10*log\left(\frac{40 W}{P_2}\right) [dB]10^{(2,5)} = 10^{log\left(\frac{40 W}{P_2}\right)}10^{(2,5)} = \frac{40 W}{P_2}P_2 = \frac{40}{316,23} = 0,1265 [W]Conclusão: Com uma potência de entrada de 0,1265 W, temos um ganho para que a saída em potência seja de 40 Watts.
b) Para a letra b temos um ganho de 40 db. Portanto seguimos os mesmos passos fornecidos acima, porém usamos a fórmula com tensão:
40 (dB) = 20*log_{10}(Av)A_v = 100
A saída de tensão Vo é dada por:
V_o = A_v * V_i
Sabendo que a potência é de 40 W, e temos que a resistência é dada por 10 ohms. Utilizaremos a potência elétrica;
P = \frac{V^2}{R}V_o^2 = P * R = 400
V_o = 20[V]
A tensão de entrada então vai ser:
V_i = 20/100 = 200 [mV]
Veja o nosso blog para mais assuntos interessantes sobre ciência e tecnologia.
Um grande abraço e fiquem em paz. Eric Serafim




