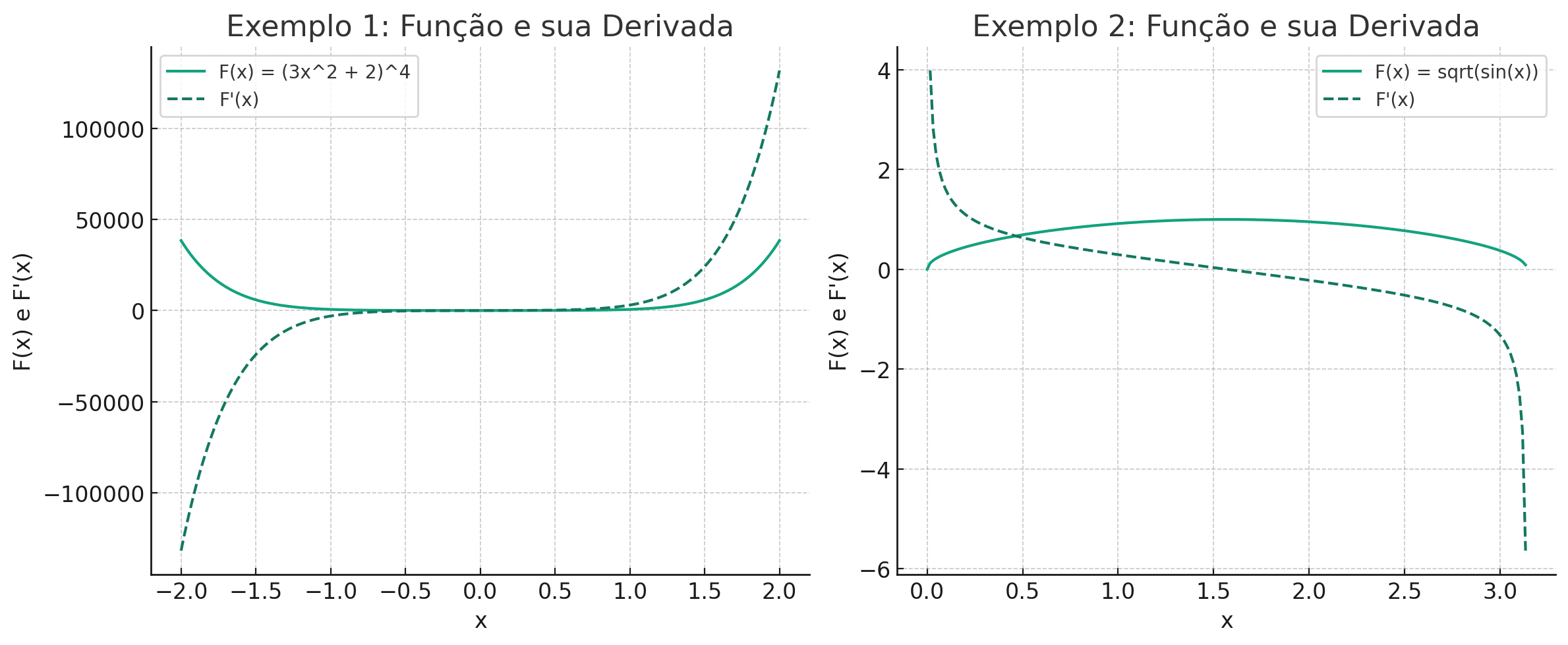
Resposta em Frequência no BJT

A resposta em baixas frequências em um BJT (transistor bipolar de junção) é afetada por muito mais parâmetros do que da aula anterior considerada.

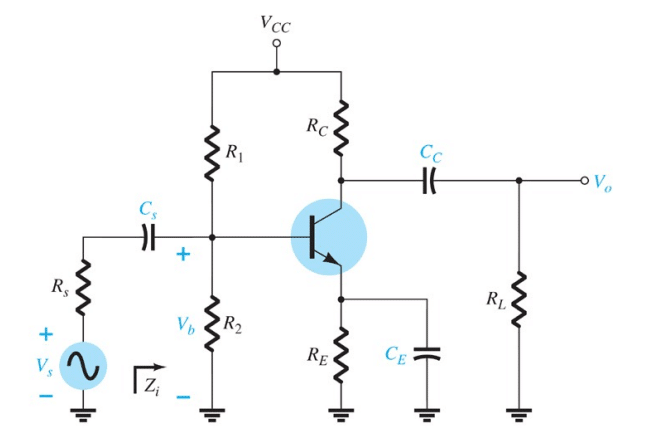
Considerando o circuito da figura abaixo, vemos que temos um circuito elétrico constituido de transsitores, capacitores e resistores.

A impedância dos capacitores não afetavam o ganho do sistema elétrico em frequências médias.

Agora as impedâncias dos capacitores serão considerados, uma vez que os mesmos afetam o ganho da resposta em frequência;

Essa condição somente aplica-se à frequências abaixo da frequência de corte do diagrama de Bode.

Frequência de Corte do Capacitor de Acoplamento (Cs)

A partir do capacitor de aclopamento (Cs) podemos determinar a frequência de corte;

Esse tipo de capacitor gera um efeito de filtro de frequências passa altas;

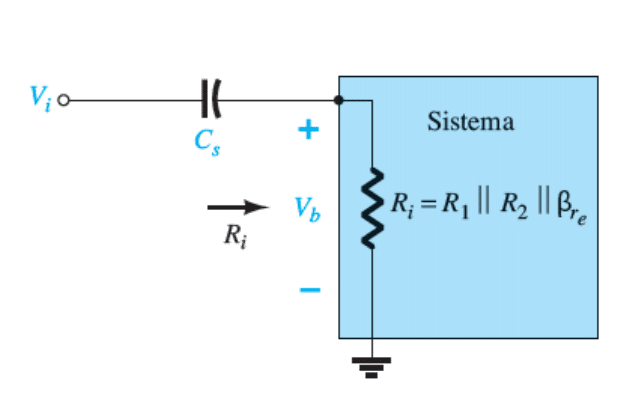
Vejamos que a resistência de entrada depende de alguns parâmetros para a figura abaixo:

R_i = R_1 || R _2 || \beta .r_e

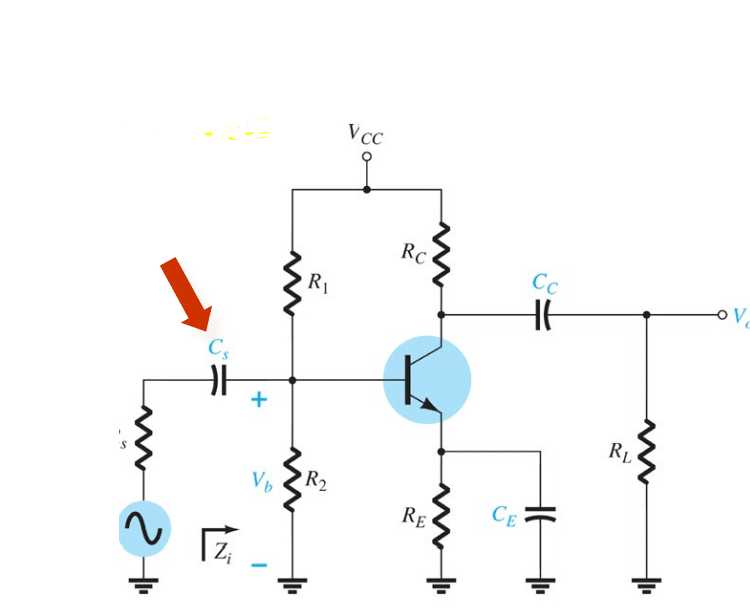
A frequência de corte do capacitor de aclopamento é dado por:

f_{ls} = \frac{1}{2\pi(R_i+R_s)C_s}

Vejamos que caso haja uma resistência interna Rs, esse valor também afetar tanto a frequência de corte como o diagrama de Bode.

O circuito equivalente fica da seguinte maneira:

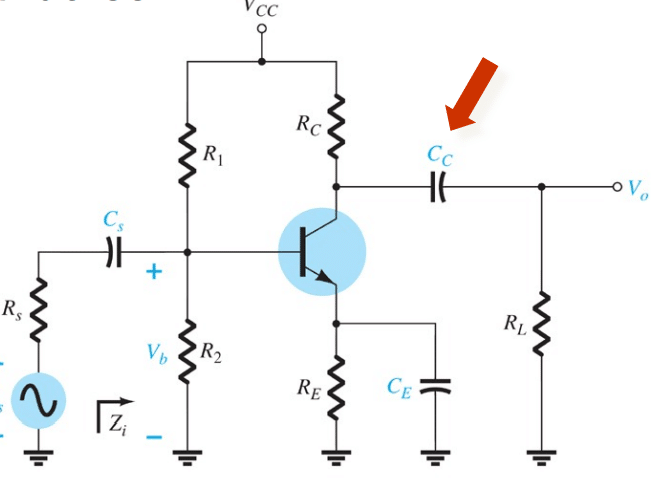
Capacitor de Aclopamento da Saída (Cc)

É o capacitor que está na saída do sistema elétrico. Vejamos na figura abaixo:

A relação dos valores das resistências são dadas por:

R_o \to R_c  \text{ Aproximadamente...}

Assim calcula-se a frequência de corte do capacitor de aclopamento na saída da seguinte maneira:

f_{ls} = \frac{1}{2\pi(R_o+R_L)C_c}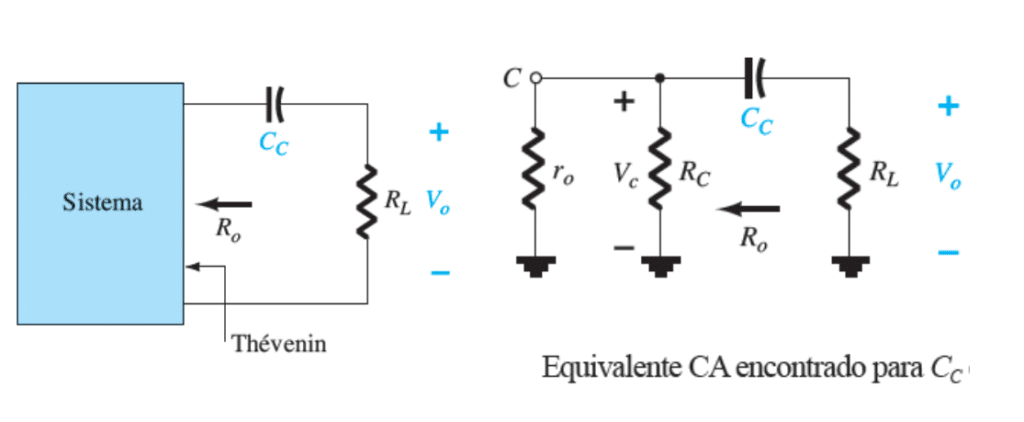

Aplicando Thévenin, podemos encontrar um circuito equivalente CA para o capacitor Cc, desse modo podemos ver algumas variáveis que antes estavam abstratas, como por exemplo r_o.

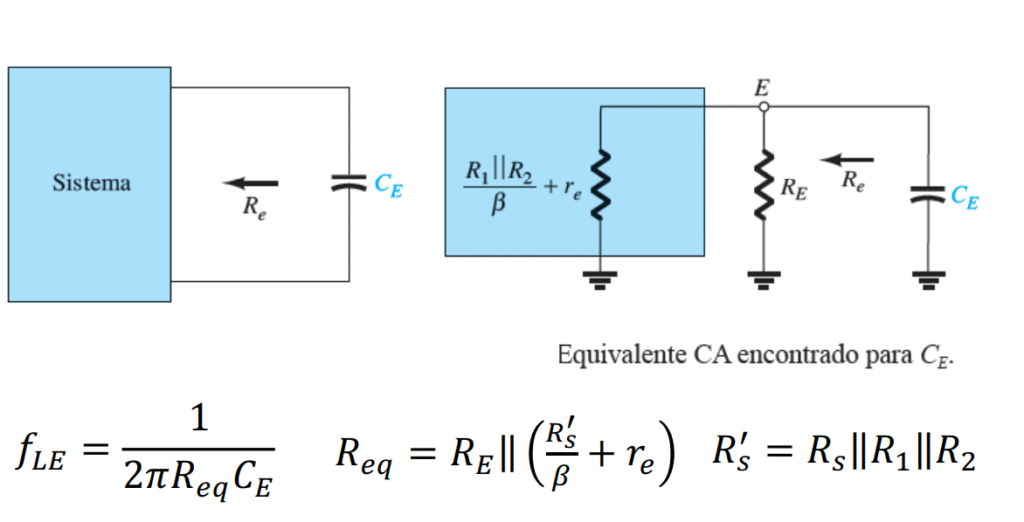
Capacitor de Aclopamento (Ce)

O capacitor de aclopamento Ce serve também como um filtro passa alta.

Dado reflexo da resistência de entrada no BJT, temos a resistência R_e = R_E || \left( \frac{R'_s}{\beta}+ r_e \right)

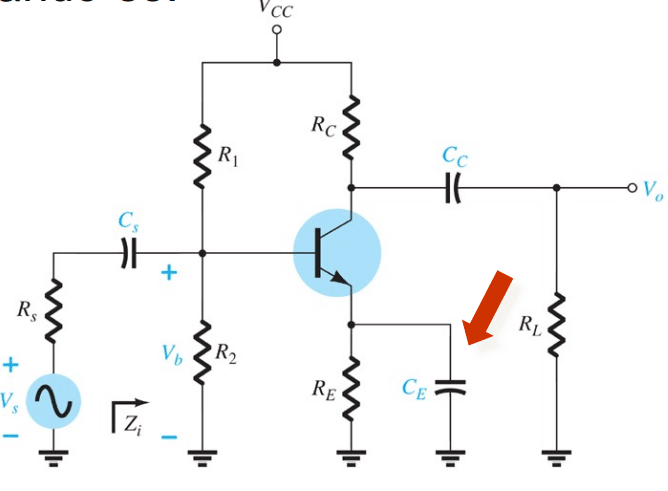
Onde R'_s = R_s || R_1 || R_2.

Portanto temos a frequência de corte nesse resistor como:

R_{eq} = R_E || R_1|| R_2

Efeito de Ce no Ganho:

Caso não haver um capacitor C_E, podemos calcular o ganho como:

A_v = \frac{-R_c}{r_e + R_E}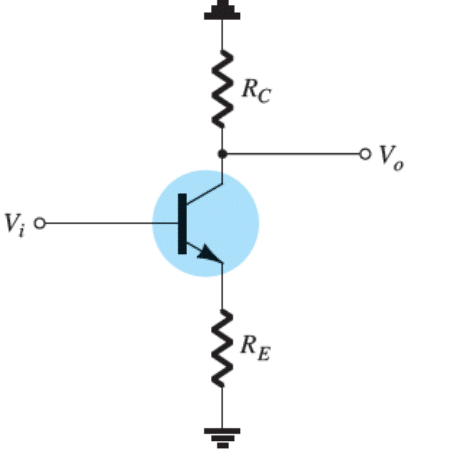

Pode acontecer de haver um capacitor C_E no qual tem uma impedância desprezível em relação á resistência R_E, desse modo o capacitor se transforma em um curto circuito, no qual a corrente só irá para C_E e não para R_E.

Assim, torna-se:

A_v = -\frac{R_c}{r_e}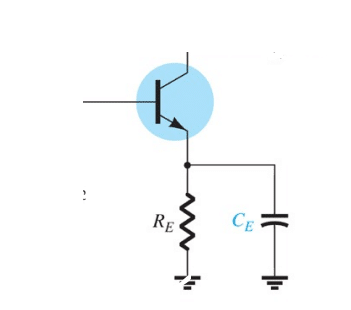

A medida que o capacitor vai ganhando carga (armazenamento de energia elétrica), ou seja, diminuindo a frequência, o valor da impedância do capacitor vai aumentando gerando uma atenuação no ganho, desse modo o ganho da segunda fórmula vai indo até o valor final dado pela primeira fórmula do ganho.