Coordenadas Tridimensionais

Um sistema de coordenadas tridimensionais é um conjunto de três eixos cartesianos que são usados para localizar pontos no espaço tridimensional. Cada ponto no espaço é descrito por três números, que são as coordenadas do ponto em relação aos eixos do sistema de coordenadas.

Representamos matematicamente como R3 (Espaço tridimensional).
Os eixos são geralmente chamados de eixo x, eixo y e eixo z. O eixo x é o eixo horizontal, o eixo y é o eixo vertical e o eixo z é o eixo que sai da tela para fora. As coordenadas de um ponto são dadas como um par ordenado (x, y, z), onde x é a coordenada no eixo x, y é a coordenada no eixo y e z é a coordenada no eixo z.

No sistema de coordenadas cartesianas, os eixos x, y e z são todos ortogonais entre si, ou seja, são perpendiculares um ao outro. Isso significa que os eixos formam ângulos de 90 graus entre si.

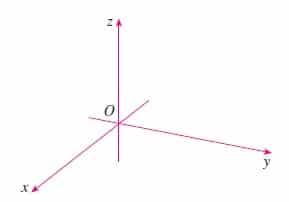
A combinação de pares de eixos entre os 3 eixos de coordenadas gera um plano. Podemos descrever 3 planos: Oxy, Oxz e Oyz, descrito na figura abaixo:

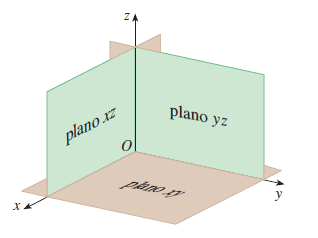
Portanto um ponto qualquer pode ser representado como P(x,y,z), onde x, y e z são as coordenadas do ponto no espaço tridimensional.

Alebricamente podemos expressar da seguinte forma:

𝑅 𝑥 𝑅 𝑥 𝑅 = 𝑅³ ={(𝑥, 𝑦, 𝑧) | 𝑥, 𝑦, 𝑧 𝜖 𝑅³}

Exemplos Resolvidos

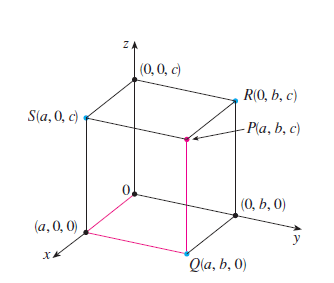
Exemplo 1: Faça um esboço de um Espaço R³ e localize um ponto qualquer P(a, b, c) nesse espaço:

Exemplo 2: Localize os seguintes pontos na superfície R³ Retângular: (0,0,c); (0,b,c); (0,b,0); (a,b,0); (a,0,0); (a,0,c), (a,b,c).

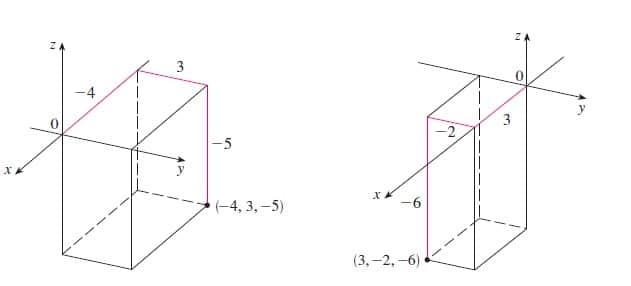
Exemplo 3: Faça um esboço em R³ e localize os seguintes pontos P1 (-4, 3, -5) e P2 (3, -2, -6):

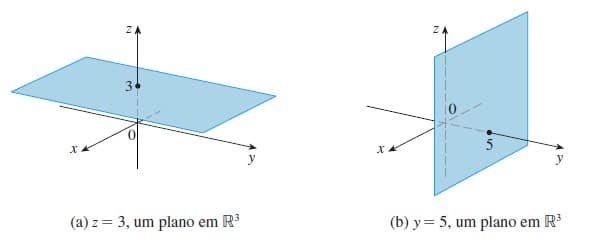
Exemplo 4: Represente as superfícies descritas pelas seguintes equações:
{(x,y,z)| z = 3} em R³ {(x,y,z)| y = 3} em R³