O ponto de máximo e mínimo das funções podem ser calculadas utilizando derivadas.
Nesse artigo vamos abordar um conteúdo de extrema importância, e saber realizar aplicação de derivadas para prever o comportamento da função e descobrir pontos críticos, máximos e mínimos globais, e locais é um baita de um conhecimento útil. Acredite em mim.
A partir dos máximos e mínimos podemos realizar otimização de processos, prever comportamentos de sistemas e análises completas de uma função definida.
- Qual é o formato de uma piscina que minimiza o uso de materiais para sua construção, mantendo um volume fixo de água?
- Como maximizar a eficiência do combustível em um carro ao ajustar a aceleração e a velocidade durante uma viagem?
- Qual deve ser o formato de uma asa de avião para maximizar a sustentação e minimizar o arrasto?
- Qual é a forma mais eficiente de um prédio para minimizar a perda de calor e maximizar o uso da luz natural?
- Qual é a dose de medicamento ideal que maximiza o efeito terapêutico e minimiza os efeitos colaterais?
- Como maximizar a quantidade de energia gerada por um painel solar ao ajustar seu ângulo de inclinação ao longo do dia?
Ponto de Máximo e Mínimo de uma função:
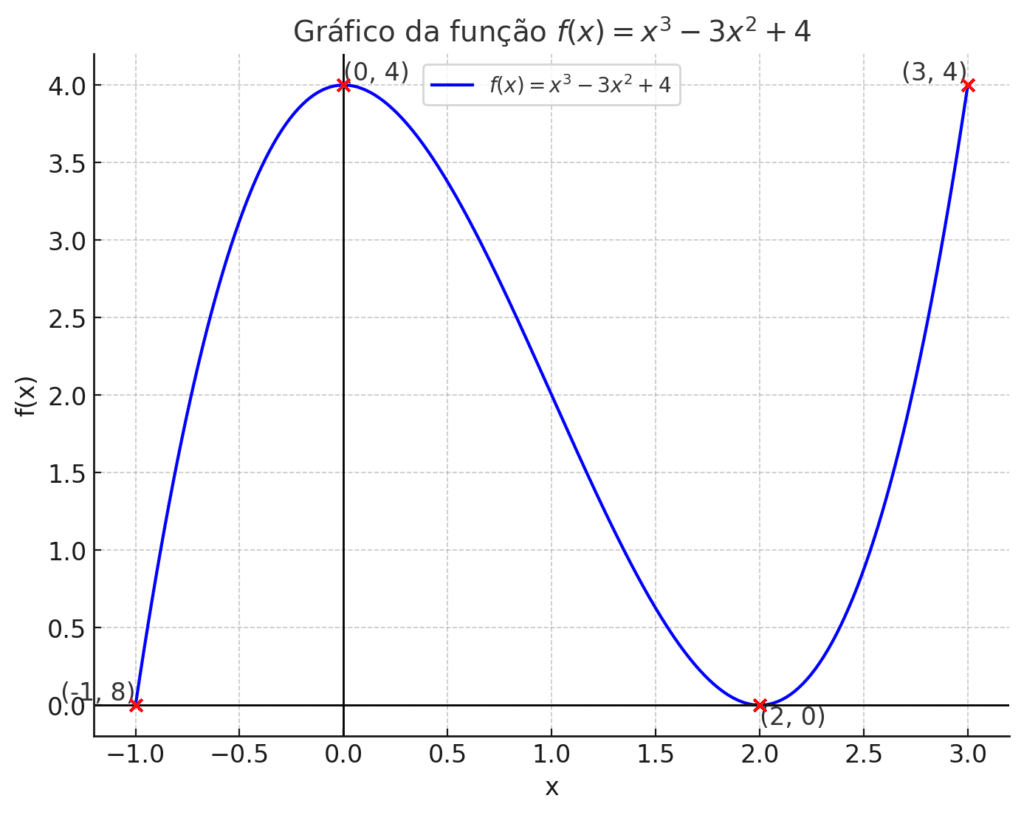
Os pontos de máximos e mínimos são da função ao lado é:
\text{Pontos de máximo: } (0,4), (3,4)\text{Pontos de mínimo:} (-1,0);(2,0)Ponto de Máximo e Mínimo Local:
Um gráfico pode ter vários pontos de máximos e mínimos, esses pontos de máximos e mínimos podem ser classificados como pontos de máximo/mínimo local ou pontos de máximo ou mínimo absoluto.
Um ponto de máximo ou mínimo local está sempre relacionado com um determinado intervalo. Veja o gráfico de uma função qualquer f(x) abaixo.
\text{Ponto de Mínimo local de f em I:[a,b] se } f(k) \le f(x), \text{para todo x em [a,b]} \text{Ponto de Máximo local de f em I:[a,b] se } f(k) \ge f(x), \text{para todo x em [a,b]} 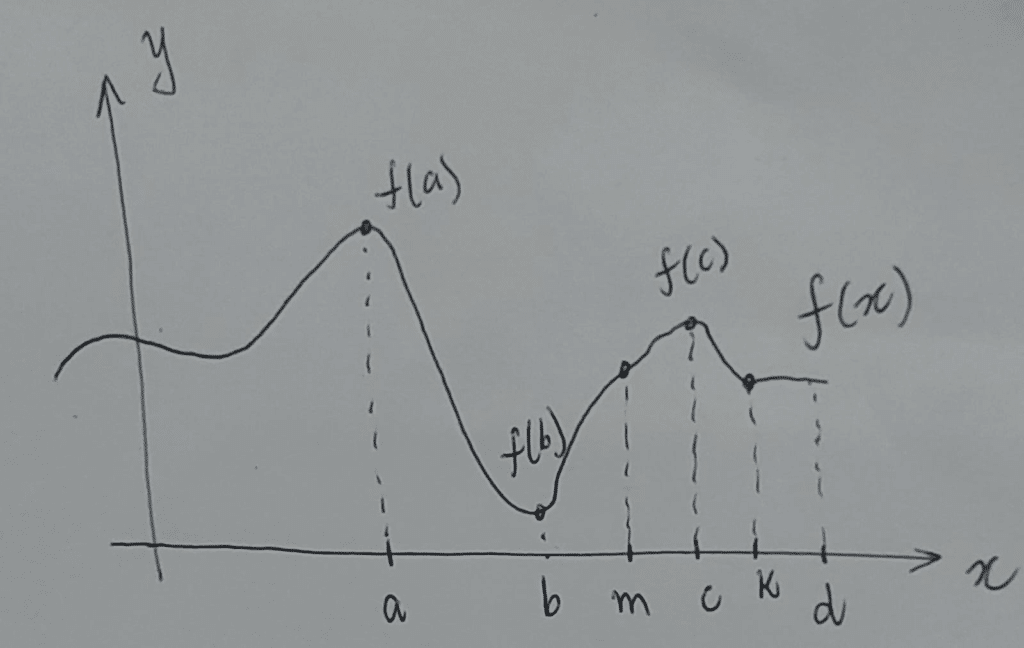
Veja que no intervalo total há:
Ponto de máximo absoluto: (a,f(a))
Ponto de mínimo absoluto: (b,f(b))
No intervalo [c,d]: Ponto de mínimo local: (k,f(k))
No intervalo [b,d]: Ponto de máximo local: (c,f(c))
Ponto de Máximo e Mínimo Absoluto:
Seja k um número que está no domínio D da função f(x). Consideramos
!ATENÇÃO! : Sempre o ”ponto de máximo ou mínimo” é de uma função em um domínio D.
Ponto de Máximo absoluto
\text{Ponto de Máximo absoluto: de f em D se } f(k) \ge f(x), \text{para todo x em D} Ponto de Mínimo absoluto
\text{Ponto de Mínimo absoluto de f em D se } f(k) \le f(x), \text{para todo x em D} 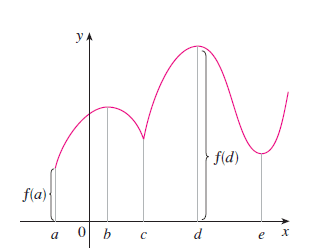
O ponto de máximo absoluto está em d e o ponto de mínimo absoluto está em a.
Justamente pois, o f(d) é o maior valor no domínio D por isso máximo.
f(a) é o menor valor no domínio D por isso Mínimo.
Teorema de Fermat:
Se f tiver um máximo ou mínimo local em k, se:
\text{1. } f'(k) \text{ existe}Se existe a derivada de f no número k. Então ele deve ser nulo.
\text{2. }f'(k) =0Números Críticos de uma função:
Números Críticos de uma função: Imagine um valor real K que está no domínio D. K será um número crítico se f'(k) = 0 ou f'(k) não existe.
Definição: Considerando uma função f(x), se em x = k, f(k) é um ponto de máximo ou mínimo, então k também é um número crítico.
Explicação: Veja que um ponto de máximo sempre é o cume da curva. Ou seja, a curva sobe, atinge o ponto de máximo e depois desce. Isso significa que nesse ponto de transição f'(x) = 0 . Do mesmo jeito, um ponto de mínimo, a curva desce até determinado ponto e depois passa a subir, novamente, inevitavelmente, f'(x) = 0 .
Exemplo 1: f(x) = |x|
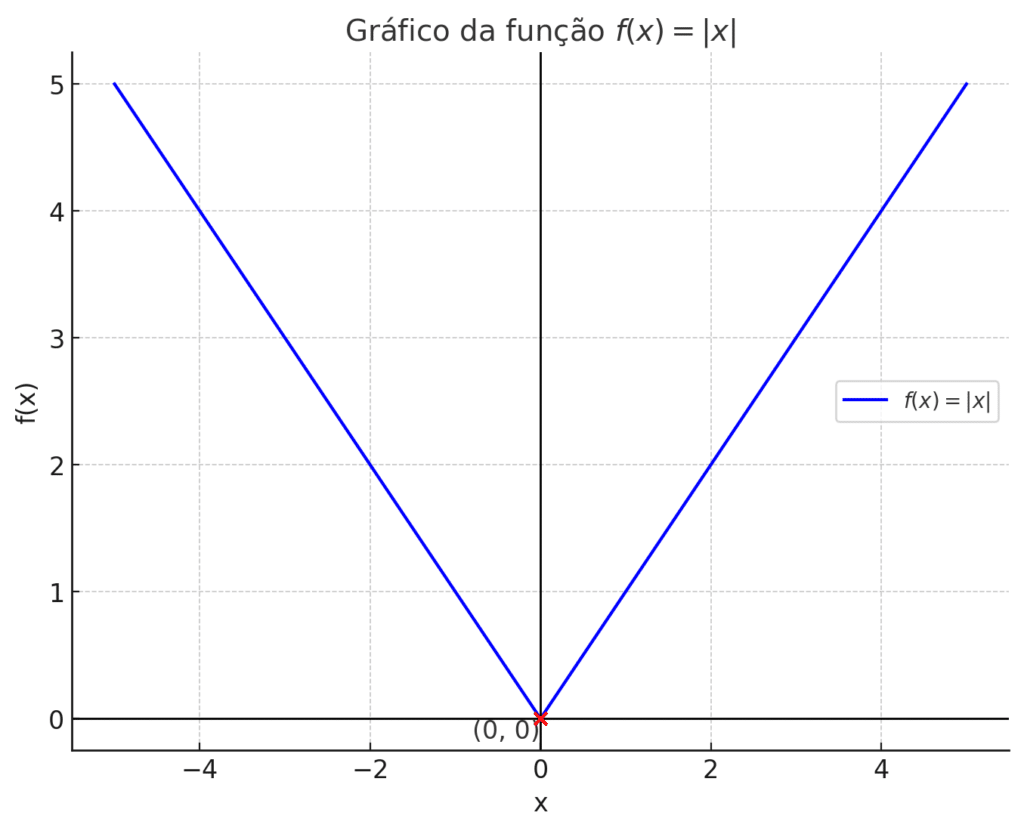
O módulo de x é representado da seguinte maneira:
f(x) =
\begin{cases}
x, & \text{se } x \geq 0 \\
-x, & \text{se } x < 0
\end{cases}
Um ponto crítico é onde a derivada da função é zero ou onde a derivada não existe. Para a função módulo, o único ponto crítico é x=0 Isso acontece porque:
- Para x>0, f(x) = x. f'(x) = 1
- Para x<0, f(x) = -x. f'(x) = -1
Desse modo. f'(x) para x = 1 não existe, pois suas derivadas se diferem em relação aos seus limites laterais.
Método do Intervalo Fechado:
Esse método é utilizado para encontrar os pontos de máximos e mínimos absolutos de uma função f(x) contínua f em um intervalo fechado [a,b]:
- Encontre os valores de f nos pontos críticos do intervalo aberto (a,b)
- Encontre os valores de f nas extremidades de D. Ou seja: f(a) e f(b)
- O maior valor encontrado é o máximo absoluto e o menor desses é o mínimo absoluto.
Exercícios Resolvidos:
1) (STEWART, James. Cálculo. 7ª ed) Encontre os valores máximos e mínimos absolutos da função.
f(x) = x^3-3x^2+1
\text{Intervalo I:}\left[-\frac{1}{2}, 4\right]A função é contínua dado esse intervalo, portanto, todas as derivadas nesse intervalo também existem.
Solução:
Passo 1: Encontrar os números críticos da função e calcular sua imagem
Para isso é necessário derivar a função e igualar a zero e encontrar os valores x em que f'(x) é 0.
f'(x) = 3x^2 - 6x = 0
Colocando a função derivada em evidência:
3x(x-2)=0
Desse modo são números críticos: x =0 e x=2.
Então:
\boxed{f(0) =0^3 -3*0^2 +1 =1}\boxed{f(2) = 2^3 -3*2^2 +1 =-3}Passo 2: Calcular f nas extremidades. x = a e x = b
Para x = a = -0,5:
f \left( -\frac{1}{2} \right) =\left( -\frac{1}{2} \right)^3-3\left( -\frac{1}{2} \right)^2 +1 \boxed{f\left( -\frac{1}{2} \right) = \frac{1}{8}}Para x = b = 4
\boxed{f(4) = 4^3 -3.4^2+1 =17}Comparando todos os valores calculados (1, -3, 1/8, 17). Podemos afirmar pelo método do intervalo fechado que:
Ponto de máximo absoluto: f(4) = 17
Ponto de mínimo absoluto: f(2) = -3
Comentários finais:
Espero que com esse artigo você consiga identificar pontos de máximos locais e pontos de mínimos locais utilizando derivadas e entendendo esses conceitos da base do estudo do comportamento das funções.
Veja que é um passo a passo a ser aplicado. Mas você deve relembrar como derivar funções.
Não se esqueça de beber água enquanto estiver estudando.
Recomendações:
https://www.uel.br/projetos/matessencial/superior/calculo/maxmin/mm02.htm
https://tutorial.math.lamar.edu/classes/calcI/minmaxvalues.aspx




