Nesta aula vamos ver um pouco sobre as relações matemáticas que há entre as funções circulares. Por hora vamos falar sobre a relação entre seno, cosseno e tangente.
Relação fundamental da trigonometria:
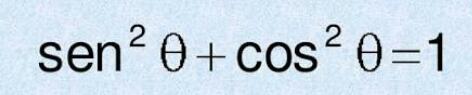
Soma dos quadrados de seno e cosseno sempre é 1. Observe que o ângulo não muda nada dessa equação, desde que os ângulos de seno e cosseno sejam iguais.
Prova da relação fundamental:
Considerando o triângulo retângulo ABC:
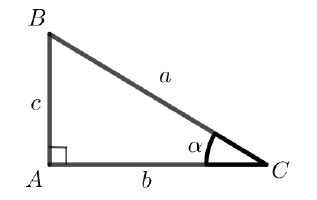
Vamos utilizar o teorema de Pitágoras: a2 = b2+ c2
Dividindo ambos os lados por a2, vamos ter:
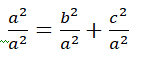
Resolvendo a equação temos:
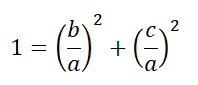
Do triângulo ABC, sabemos que:
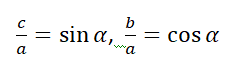
Juntando a equação 1 com a equação dois vamos chegar a relação trigonométrica que é dado por:
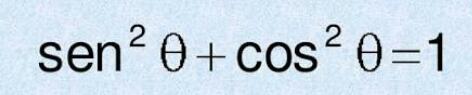
Relação entre a tangente, seno e cosseno:
A tangente de um ângulo é a razão entre seno e cosseno deste mesmo ângulo. Denotamos:
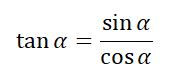
Podemos provar simplesmente fazendo essa razão com os lados do triângulo. Caso quiser ver tal prova, assista o vídeo: https://www.youtube.com/watch?v=Bqt6T0VWGoA
Nada melhor que exercícios para aprender a matéria. Veja os próximos 5 exercícios resolvidos:
Exercícios resolvidos:
1) (Mack-SP) Calcule a medida do segmento AB sabendo que BCDE é um retângulo.
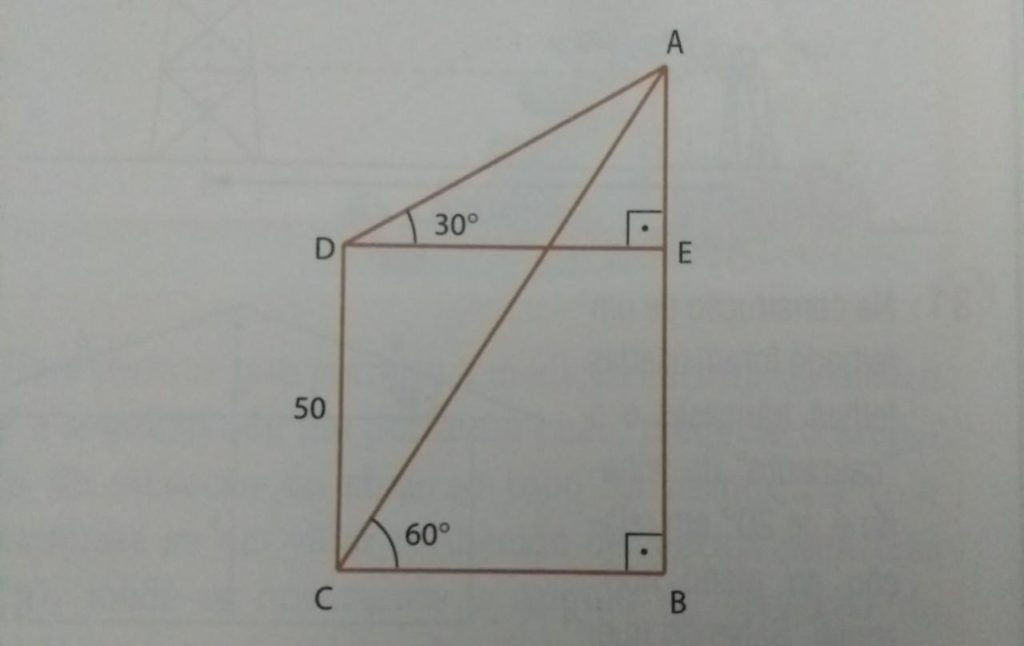

3) (UFSC) Uma escada de 10m de comprimento apoiada em uma parede que é perpendicular ao solo.Sabendo que o pé da escada está afastada a 6m da base da parede, determine a altura, em metros, alcançada pela escada.
Gabarito:







