Potencial elétrico de diversas cargas:
Considerando temos em uma certa região do espaço com n partículas com cargas elétricas:
Q1, Q2, … , Qn.
Sabemos que cada carga elétrica gera seu próprio potencial elétrico, e o nosso objetivo é calcular o potencial elétrico resultante no ponto p.
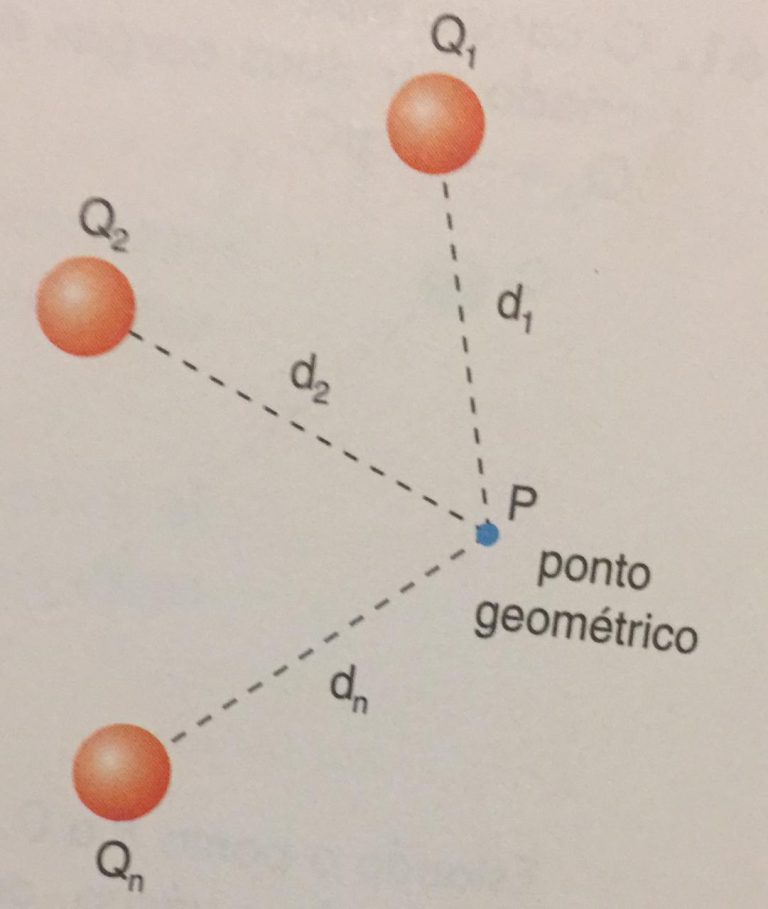
Calculando:
1) Devemos calcular o potencial elétrico gerado por cada carga em p. Usamos então a formula:
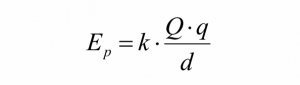
2) Devemos fazer a soma total de todos potenciais gerados pelas cargas:
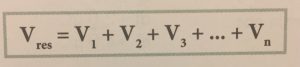
Fique esperto na hora da soma, pois potencial elétrico é um grandeza escalar, portanto ela pode ser positiva ou negativa.
Equipotenciais:
São linhas ou superfícies imaginarias que possuem o mesmo potencial elétrico. Geralmente as figuras de superfícies equipotenciais são espaciais, ou seja, tridimensionais, o que deixa muito complexo análise dos mesmos.
Considerando uma carga fixa Q, que gera um campo elétrico e um potencial elétrico sobre p, temos:
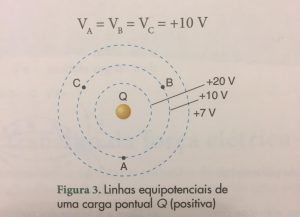
Observe que os pontos A, B, C estão na mesma linha pontilhada e portanto são equiponteciais ou seja as potencias elétricas são as mesmas!
Campo elétrico uniforme:
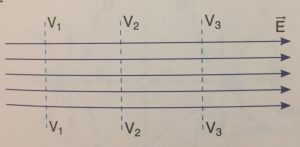
Todos os pontos que estiver na linha pontilhada, terão o mesmo potencial elétrico. Quando formos desenhar as linhas equipotenciais em um campo elétrico uniforme assim como na figura 4, as linhas equipotenciais devem ser perpendiculares as linhas de campo elétrico. Consequentemente as linhas equipotenciais são paralelas entre si, assim como as linhas de campo são paralelas entre elas.
Os exercícios também necessitam uma boa capacidade de análise, faça os execícios propostos e veja o gabarito depois!

Exercícios propostos:



Gabarito:







