Limites no infinito
Introdução:
Vão haver momentos que os limites que calcularemos irão tender ao infinito. Vimos na seção anterior assim como na aula do problema da tangente que o limite é a representação de valores do domínio chegando extremamente perto de um determinado x, onde farão um valor da imagem y tender a outro valor.
Caros alunos, fiquem com uma coisa em mente. Infinito não é um número! É somente a representação de um valor extremamente alto, ou seja, um valor suficientemente alto para receber a “representividade”de infinito. Um valor nunca é infinito! Mas tende ao infinito!
Começando com um Exemplo:
Assim como nas partes passadas, iniciaremos o assunto com um exemplo, assim podemos idealizar melhor o conceito de limites no infinito. Porém fica como um prefacio que temos uma função f(x), que quando x tende a um valor a, a função tende ir a mais ou menos infinito. Vejamos um exemplo:
lim_{x \to 0}\frac{1}{x^2} = \infty
Assim como fizemos todos os exemplos, vamos analisar um tabela de valores de x e f(x) e o gráfico da função e depois vamos tirar nossas conclusões:

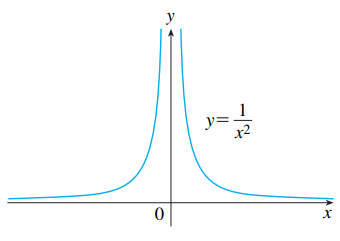
Observe primeiramente os valores de x, cada vez que os valores de x mais se aproximam de 0, mais o valor de f(x) se aproxima de um número muito muito grande! Denotamos então que f(x) -> ∞
Vejamos:
f(\pm 1) = \frac{1}{(\pm 1)^2} = 1 f(\pm 0,5) = \frac{1}{(\pm 0,5)^2} = 4 f(\pm 0,20) = \frac{1}{(\pm 0,20)^2} = 25Vemos que cada vez que x \to 0, mais f(x) \to \infty
A simbologia do infinito apenas significa que podemos deixar o valor de f(x) tão grande ou melhor, suficientemente grande, a medida que os valores de x vão se aproximando de 0.
Quando x \to 0,0000000001, temos algo como f(x) \to 100000000000000000000!
Denotamos então como:
lim_{x \to 0}\frac{1}{x^2} = \infty
Agora vamos definir os limites no infinito de forma mais formal:
Definição 4:
Seja f definido em ambos os lados de a, exceto possivelmente igual a a, denotamos:
lim_{x \to a}{f(x)} = \infty
Significa que podemos deixar os valores de f(x) arbitrariamente grandes a medida que aproximamos valores de x=a, mas não igual a a.
Do mesmo jeito que:
lim_{x \to a}{f(x)} = – \infty
Significa que podemos deixar os valores de f(x) arbitrariamente grandes, porém negativos, ao tornar x suficientemente perto de a, mas não a.
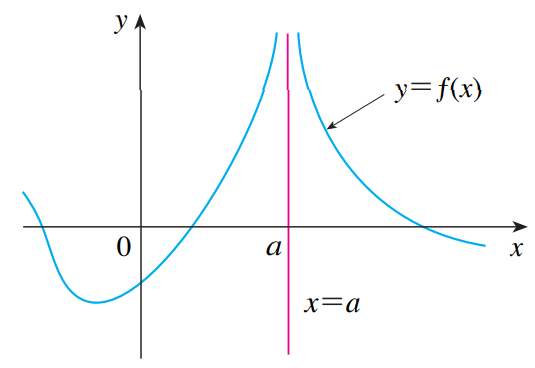
Podemos dizer:
- “O limite de f(x) quando x tende a a, é infinito.”
- “f(x) se torna infinito, quando x tente a a.“
- “f(x) cresce ilimitadamente quando x tende a a.“
Definição de limite no infinito para limites laterais:
Vimos anteriormente, que o limite de uma função f(x) pode tender a um número suficientemente grande, que damos como termo o infinito. Essa definição funciona para os limites laterais, ou seja, caso o limite estiver se aproximando pela esquerda ou pela direita, e ainda sim tendem a mais ou menos infinito. Veja os exemplos:
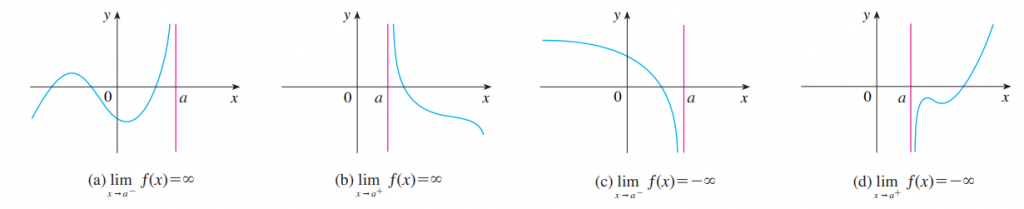
Definição 5:
A reta x = a é chamada de assíntota vertical da curva y = f(x) se pelo menos uma das condições abaixo serem satisfeitas:
1 lim_{x \to a}{f(x)} = \infty
3. lim_{x \to a^- }{f(x)} = \infty
5. lim_{x \to a^+}{f(x)} = \infty
2. lim_{x \to a}{f(x)} = -\infty
4. lim_{x \to a^-}{f(x)} = -\infty
6. lim_{x \to a^+}{f(x)} = -\infty
Observe a reta x=a nos gráficos acima, chamada de assíntota vertical, uma vez que x=a está na vertical!
Exercícios resolvidos:
Exemplo 1: Identifique qual valor do limite é negativo e qual é positivo.
a. lim_{x \to 3^+}{(x – 3)}
b. lim_{x \to 2^-}\frac{10}{x-2}
c. lim_{x \to 2^-}\frac{10}{2-x}
Solução:
Análise primária: Vemos que quando falamos de 3^+ estamos nos referindo a valores muito próximos mas maiores do que 3.
No mesmo racicínio, 2^- são valores muito próximos de 2, porém menores do que 2.
Assim, vamos aos exercícios:
a) Substituindo 3^+ em x, temos que:
(3^+ – 3) < 0 lim_{x \to 3^+}{(x – 3)} é negativo!b) no denominador: 2^- – 2 < 0 , assim:
lim_{x \to 2^-}\frac{10 (+)}{x-2 (-)} e
sabemos que positivo com negativo é negativo em uma divisão!
c) no denominador: 2^+ – 2 > 0 , assim:
lim_{x \to 2^+}\frac{10 (+)}{x-2 (+)} e
sabemos que positivo com positivo é positivo em uma divisão!
Exemplo 2: Calcule lim_{x \to 3^+}{\frac{2x}{x-3}} e lim_{x \to 3^-}{\frac{2x}{x-3}}:
Vimos que um limite de um valor dividido por zero tende para mais ou menos infinito! Vamos ver agora como funciona esses dois limites:
3^- – 3 = 0^- (um valor que se aproxima de 0 e menor do que zero, isto é, negativo)
3^+ – 3 = 0^+ (um valor que se aproxima de 0 e maior do que zero, isto é, positivo)
Poranto conclui-se que:
\boxed{lim_{x \to 3^-}{\frac{2x }{x-3}} = \frac{2*(3^-) (+)}{0^- (-) } = -\infty}
\boxed{lim_{x \to 3^+}{\frac{2x }{x-3}} = \frac{2*(3^+) (+)}{0^+ (+) } = +\infty}




