Respostas:

A lista de exercício anterior mostra claramente como resolver esses exercícios. Porém algumas coisas mudaram. Agora veja que os valores de y vão para o infinito. (Caso surgir dúvidas sugiro que leia sobre limites no infinito e a lista de exercício anterior)

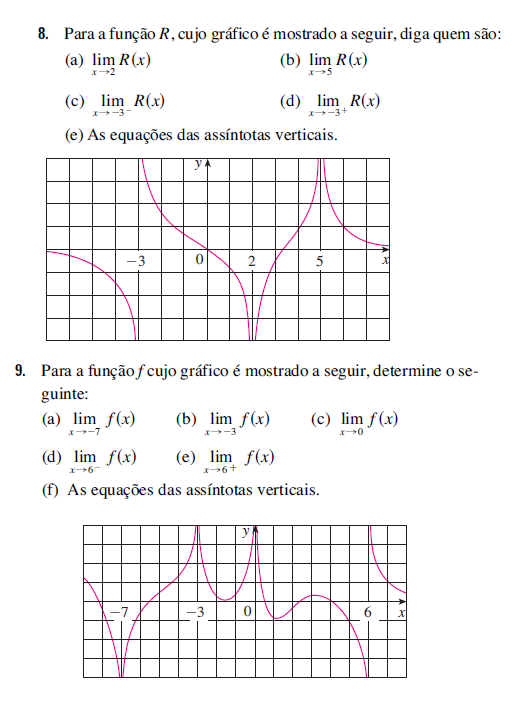
Resposta Exercício 8)

a) Olhando a vizinhança de x = 2 vemos que R(x) tende para o valor infinito negativo. Portanto:

\boxed{lim_{x \to 2}R(x) = -\infty}

b) Do mesmo jeito:

\boxed{lim_{x \to 5}R(x) = +\infty}

Agora veja como o negócio fica louco! Um dos limites laterais (pela esquerda) vai para menos infinito e o da direita vai para mais infinito portanto:

c)

\boxed{lim_{x \to -3^-}R(x) = -\infty}

d)

\boxed{ lim_{x \to 3^+}R(x) = -\infty}

Resposta Exercício 9)

Do mesmo jeito que os exercícios anteriores, vamos análisar os gráficos e resolve-los:

a) \boxed{lim_{x \to -7}f(x) = -\infty}

b) \boxed{lim_{x \to -3}f(x) = +\infty}

c) \boxed{lim_{x \to 0}f(x) = +\infty}

d) Veja que no mesmo caso da letra c) e d) do exercício 8, temos limites laterais com valores diferentes.

\boxed{lim_{x \to 6^-}f(x) = -\infty}

e)

\boxed{lim_{x \to 6^+}f(x) = +\infty}

f) Agora vejamos as assintotas verticais. Podemos expressar elas não de acordo com y(x) mas sim de acordo com uma reta em x. Ou seja; Vamos dizer onde essas assíntotas verticais estão em x, essas serão as equações das A.V.

portanto:

\boxed{ x = – 7}

\boxed{x = – 3}

\boxed{x = 0}

\boxed{x = 6}

Lembre-se que as curvas e as assíntotas nunca se encostam!