Vimos na aula passada, que existe uma propriedade dos limites chamada de substituição direta, no que consiste em calcular limites de funções simplesmente substituindo x para a. Funções que permitem o uso dessa propriedade, são também classificadas como funções contínuas.
Uma função é sempre descontínua em um certo ponto. Ou seja, f(x) é descontínua quando x é igual a 4, por exemplo!
Definição 1:
Uma função é contínua em um ponto a, se somente se:
lim_{x \to a}f(x) = f(a)
Para essa condição ser satisfeita, implicitamente 3 condições:
a) f(a) deve estar definida; a deve estar no domínio de f
b) lim_{x \to a}f(x) deve existir!
c) lim_{x \to a}f(x) = f(a)
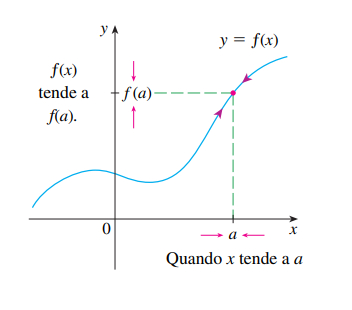
Observação: Uma função sempre é contínua em um ponto.
Exemplo 1: Gráfico
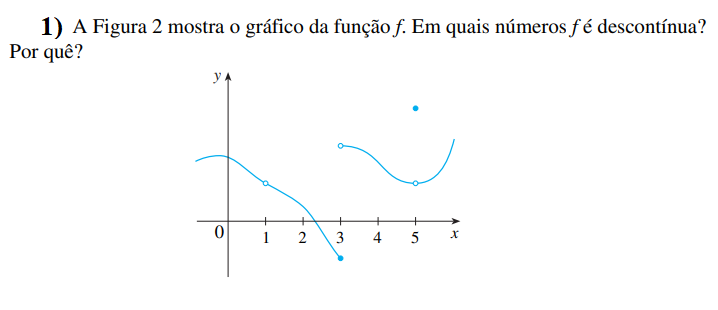
Para resolvermos esse tipo de exercício de continuidades de limites na forma gráfica, é preciso analisar os pontos que apresentam uma “quebra”. Veja que as partes dos gráficos que são linhas “desenhadas bonitinhas” são contínuas, então devemos dar atenção somente em pontos específicos, como x =1, x = 3 e x =5.
Pelo gráfico já pelo gráfico, já percemos que a “bolinha não preenchida” é um ponto não definido em x = 1, portanto não há continuidade. De modo que:
\boxed{f(1) = \nexists}
No ponto x = 3, veja que o limite de f(x) quando x tende a 3 não existe! Portanto f(x) é descontínuo em x = 3. (condição de existência de um limite), pois:
\boxed{lim_{x \to 3^-}f(x) \ne lim_{x \to 3^+}f(x)}
Já para x = 5, vemos que o limite existe e o ponto também está definido, porém infringe a principal condição de continuidade, pois:
\boxed{lim_{x \to 5}f(x) \ne f(5)}
Veja bem o gráfico! Mesmo sem saber qualquer valor, podemos analisar isso!
Exemplo 2: Algebrico

Para resolvemos exercícios de continuidade (ou descontinuidade) de forma algebrica devemos descubrir primeiro qual é o domínio de f(x), ou, onde uma função se comporta de forma diferente. Vamos ver nos exemplos esses tipos de situações.
______________________________________________________________________________________
a) f(x) = \frac{x^2 – x – 2}{x – 2}
O denominador de um função nunca pode ser 0, e caso estiver em um limite, tende ao infinito (positivo ou negativo. Depende). Portanto, quando x = 2, f(x) não está definido. Assim, f(2) não existe e é uma descontinuidade.
______________________________________________________________________________________
b) f(x) =\begin{cases}\frac{1}{x},\text{ se } x \ne 0 \\ 1, \text{ se } x = 0 \end{cases}
Vemos que a função se comporta em diferentes leis quando x = 0 ou diferente desse valor. Portanto devemos analisar quando x = 0.
Vamos testar as condições propostas nessa aula:
f(0) está definida? Sim! e f(0) = 1, visto na função por partes.
O limite existe? Não existe! Vejamos que esse limite vai até o infinito, ou seja, não existe!
lim_{x \to 0^-}{\frac{1}{x^2}} = +\infty
lim_{x \to 0^+}{\frac{1}{x^2}}= +\infty
Portanto, f(x) é descontínuo quando x = 0.
______________________________________________________________________________________
c) f(x) =\begin{cases}\frac{x^2 – x – 2}{x – 2},\text{ se } x \ne 2 \\ 1 , \text{ se } x = 2 \end{cases}
Agora nesse caso, a função muda de comportamento quando x = 2. Desse modo:
f(x) está definido em x = 2? Sim! f(2) = 1.
O limite de f(x) quando x tende a 2 existe? Vamos calcular esse limite? Para isso lembre-se que devemos utilizar manipulação matemática para evitar indeterminações. (Clique aqui para relembrar)
Vamos lá. Pelo método da substituição direta, o limite ficará assim:
lim_{x \to 2}{\frac{x^2 – x – 2}{x – 2}} = \frac{(2)^2 – 2 – 2}{2 – 2} = \frac{0}{0} \to indeterminação
Vamos fatorar a função quadrática e tentar simplificar alguma coisa.
\text{Vamos calcular as raízes da expressão} x^2 – x – 2 = 0 \\\text{Delta e Bhaskara:} \\ \Delta = b^2 – 4ac \\ \Delta = (-1)^2 – 4(1)(-2) = 9 \\x = \frac{-b \pm \sqrt{ \Delta}}{2a} \\ \text{portanto temos:} \\ x = \frac{-(-1) \pm\sqrt{ 9}}{2} \\
\boxed{x_0 = +2} \boxed{x_1 = -1}
Como parte da fatoração, podemos expressar uma função de segundo grau da seguinte forma:
ax^2 + bx + c = a*(x – x_0)*(x – x_1)
Portanto podemos expressar a função quadrática do numerador como:
x^2 – x – 2 = 1.(x – 2)(x + 1)
Agora que modificamos o numerador, podemos voltar ao limite:
lim_{x \to 2}\frac{(x – 2)(x + 1)}{x – 2} = lim_{x \to 2}\frac{\cancel{(x – 2)}(x + 1)}{\cancel{x – 2}}\boxed{lim_{x \to 2}{(x + 1)} = 3}
E assim chegamos na condição 3! O limite de x tendendo a 2 é igual a f(2) ? Não!!
pela função dada em questão f(2) = 1 assim:
{lim_{x \to 2}f(x) \ne f(2)}
Portanto a função em questão é descontínua em x = 2.
Conseguimos desenhar os 3 gráficos do exemplo 2 (a,b,c), para os gráficos que são contínuos, observe que podemos desenha-los sem tirar a caneta do papel, pois é uma linha contínua, não há saltos.
Todos os exercícios do exemplo 2 deram em descontinuidades. Veja que é impossível conseguir desenhar o gráfico sem tirar a caneta do papel. Pois todas essas funções (olhe os gráficos abaixo) são funções descontínuas em determinados pontos.
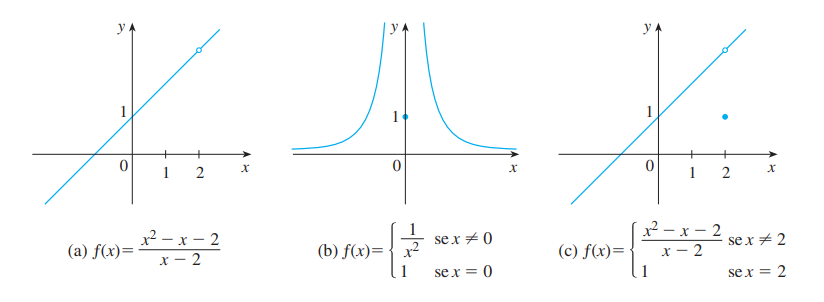
Definição 2:
Podemos definir a continuidade da direita e à esquerda de uma função.
A função é contínua a direita dela mesma se:
lim_{x \to a^+}{f(a)}
A função é contínua a esquerda dela mesma se:
lim_{x \to a^-}{f(a)}
Definição 3:
A função f(x) é contínua em um intervalo, se somente se, a função f(x) for contínua em todos os pontos que pertencem a esse intervalo.
Exemplo 3:
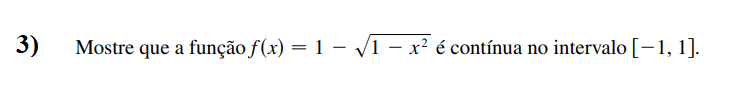
Quando estamos analisando uma função raíz, temos que ter certeza de que o valor dentro raíz seja igual a zero ou positivo. Caso o valor for negativo dentro da raíz estamos em outro conjunto matematico que são os números complexos.
Portanto, para f(x) ser contínuo, 1 – x^2 \ge 0, assim temos uma inequação para resolver. De forma que:
1 – x^2 \ge 0
1 \ge x^2
\boxed{-1 \ge x \ge +1}
Em outras palavras, x deve estar entre -1 e 1. Caso o valor de x = 1,1, o valor seria negativo e gerando uma descontinuiadade.
Assim mostra-se que no intervalo x [-1, 1] a função é contínua, sem quebras, pontas ou valores diferentes. Com intervalo x [-1,1] temos que:
lim_{x \to [-1,1]}{f(x) = f(x = [-1,1])}
Mostra-se então de f(x) é contínua nesse intervalo.
Teorema 1:
Se as funções f e g forem funções contínuas em a, c é uma constante, as seguintes funções, também serão contínuas:
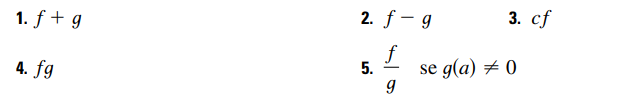
Teorema 2:
b) Qualquer função racional é contínua para todo x pertencente ao seu domínio.
Exemplo 4:
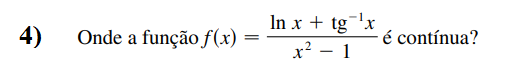
Baseado no teorema 1 temos que há diversas funções que se todas forém contínuas, f(x) será contínua também. Portanto devemos estudar o domínio de todas as funções, e associar esse conjunto domínio para chegarmos em valores em que x se encaixam em todas as funções!
Vamos cada função:
ln(x), x deve ser positivo \to x = (0,+\infty)
x^2 – 1 \pm 0, portanto x \ne \pm 0
Para a função tg(x) devemos relembrar que:
tg^-1 (x), x (0,+\infty)
Portanto:
O domínio da função em total: x = (0, 1) U (1, +\infty)
Teorema 3:
As funções abaixo, são funções contínuas para to x contínuo em seu domínio natural, entre elas são:
- Polinômios
- Funções Trigonométricas
- Funções Exponenciais
- Funções Racionais
- Funções Trigonométricas Inversas
- Funções Logarítmicas
- Funções Raízes
Teorema 4:
Se g for contínua em a, e f for contínua em g(a), temos que a função composta f(g(x)) também é contínua.
Teorema do valor intermediário:
Supondo que f seja contínuo em um intervalo fechado [a,b], seja N entre os valores de f(a) e f(b) em que: f(a) ≠ f(b), então existe um valor c em (a,b) tal que: f(c) = N.
Então basicamente temos um valor N entre dois valores f(a) e f(b), devemos ter um valor c entre o a e b, para corresponder ao valor N. (f(c) = N).
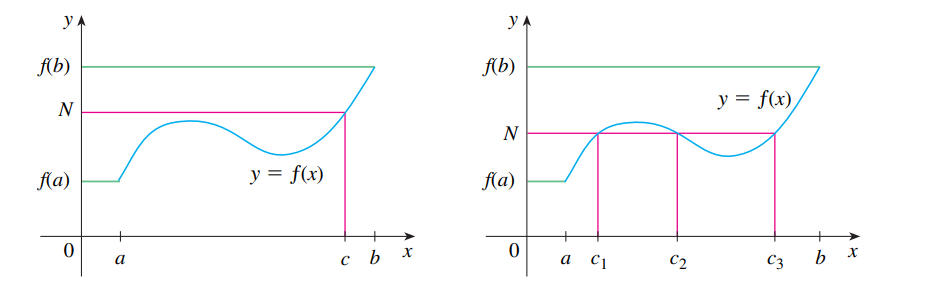
Uma das grandes aplicações do teorema do valor médio, é encontrar valores próximos de raízes de funções, ou até mesmo um valor exato, caso existir.




