Introdução:
As derivadas podem ser interpretadas como taxas de variação, no que é muito utilizadas tanto na ciência como na engenharia.
Parte 1 - Tangentes:
Se uma curva C que contenha um ponto P(a, f(a)) e um ponto genérico Q(x, f(x)). Para calcularmos a reta secante do ponto P e Q temos:
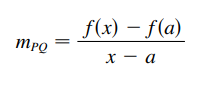
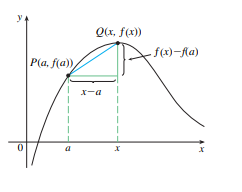
Mas agora, se quissemos calcular a reta tangente que passa pelo ponto P(a, f(a))? Bom, se temos o ponto P, devemos ter a inclinação da reta m, assim podemos descobrir a equação da reta tangente que passa por P.
Estratégia: Vamos aproximar o ponto Q cada vez mais perto do ponto P. Na prática iriamos calculando diferentes inclinações de reta (m=Δy/Δx) a medida que Q se aproxima de P. Vamos definir quando Q é suficientemente próximo de P (Q->P):
Definição 1:
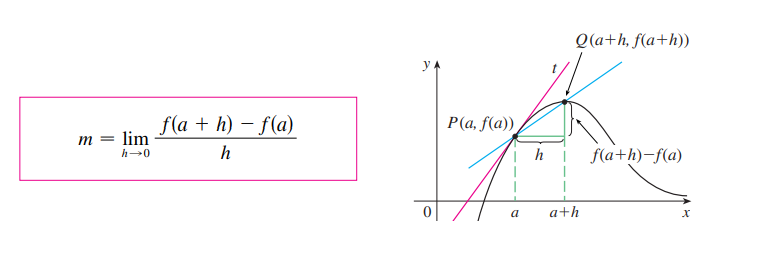
A reta tangente de c, y=f(x) no ponto P(a, f(a)) é a reta com inclinação:
desde que o limite exista.
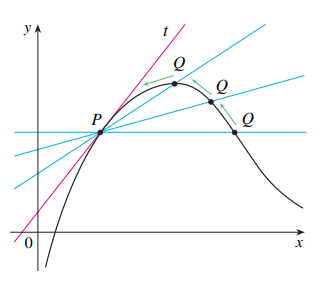
Observe a figura 2, são mostradas as retas secantes PQ, a medida que Q se aproxima de P, e olhe que as retas gradualmente estão cada vez mais próximas de ser a reta tangente no ponto P. A definição 1, é muito intuitiva uma vez que quando Q está suficientemente próximo de P, a inclinação da reta é a inclinação da tangente do ponto P.
Exemplo 1:
Visto no gráfico anterior e a definição 1, podemos mudar as variáveis do limite.
O limite definido previamente é dado por:
Que não é nada a mais que a inclinação da reta tangente que passa pelo ponto P.
No gráfico abaixo podemos dizer que h=x-a. portanto x=h+a. Fazendo uma substituição de variável no limite temos:
f(x) = f(h+a) então:
A inclinação da reta secante PQ é dado por: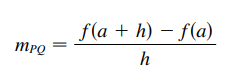
A inclinação da reta tangente que passa por P:
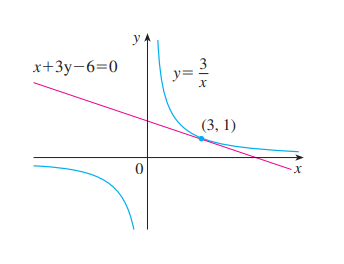
Exemplo 2:
Parte 2 - Velocidade:
Suponhamos que um objeto se desloque sobre uma linha reta de acordo com a função s=f(t) tal que:
s=deslocamento do objeto a partir da origem em função do instante t.
s=f(t) -> função posição do objeto
Imagine uma reta que representa a posição de um objeto (s), e cada ponto da posição está em função de um instante (t). Observe a figura abaixo:
Na figura a cima em s(t) = s(a) = f(a) e s(t)=s(a+h)=f(a+h).
A variação de espaço é dado por espaço final menos o espaço inicial = Δs= f(a+h) – f(a).
a variação de tempo é dado pelo instante final menos o instante inicial = Δt= (a+h)-a = h.
e a velocidade media é v=Δs/Δt, substituindo as primeiras equações na equação da velocidade, obtemos:
Velocidade instantânea:
Considerando agora que o instante inicial to vai se aproximando do instante final t, e quando to chega suficientemente próximo de t, tal que dizemos que to tende a t ou seja to->t dizemos que o limite da função espaço s(t) quando to->t é a velocidade instantânea do instante t.
Modificando algumas variáveis:
to = a
também vimos que: (to->t) logo: to= t
Se t= a+h e t = to tal que to=a.
Com a segunda equação: a+h= a; então h->0
Simbologicamente podemos dizer que: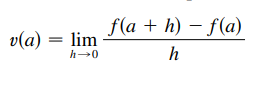
Exemplo 3:
Parte 3 - Derivadas:
As derivadas podem representar muitas coisas, como por exemplo: a inclinação de uma reta, além disso é muito usado para diversos cálculos de variações que acontecem na química, física, economia e etc.
Definição 2:
A derivada de uma função f(a) é denominada: f´(a), tal que, definimos: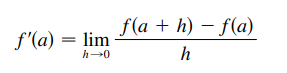
o limite deve existir!
Outra forma de escrever a derivada de uma função:
Vamos determinar outra forma de escrever o limite dado acima, representando a derivada de um função f. Vamos chegar nesse novo limite por substituição de variáveis:
Portanto vamos alterar algumas coisas:
consideremos x = a+h , portanto h=x-a, se h->0 concorda que o valor de x tem que tender a a (x->a)? Então:
Dizemos que:
f(a+h) = f(x); f(a) = f(a) e h = x-a; Portanto a equação acima da seguinte maneira:
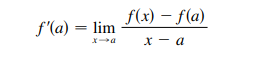
Exemplo 4:
Equação da reta com um ponto P(a, f(a)) e f`(a):
Exemplo 5:
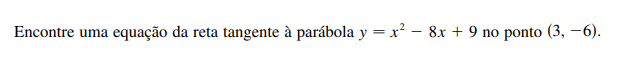
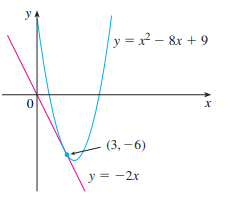
Parte 4 - Taxas de variação:
Vamos considerar a variação de x e de y, então:
Δx = x – xo
Δy = y – yo = f(x) – f(xo)
A razão entre as Δy e Δx é dado por:
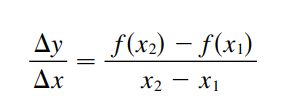
Observe que essa razão é a mesma coisa que a tangente da reta que liga esses pontos que também é a inclinação dessa reta.
Quando Δx->0 , temos que essa razão tem o significado de uma taxa de variação instantânea – no instante – definimos então:
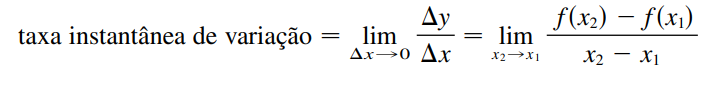
Observe também que essa equação é a representação da inclinação da reta tangente ao ponto de aproximação. E essa é uma das aplicações de quem?! Da derivada é claro! ENTÃO A DERIVADA DE UMA FUNÇÃO É A TAXA INSTANTÂNEA DE VARIAÇÃO DE f(x). Definindo:
