Existência de um Limite
Um limite pode existir ou não. A condição de existência de um limite está em sua continuidade, seu domínio e sua imagem.
Nessa aula vamos analisar e entender como funciona cada uma dessas condições no qual será de extrema importância!
Quando estamos falando de limites, podemos fazer 3 cálculos:
- Limite lateral tendendo pela esquerda; (lim_{x \to a^-}{f(x)})
- Limite lateral tendendo pela direita; (lim_{x \to a^+}{f(x)})
- Limite Bilateral; (lim_{x \to a}{f(x)})
É ai que entra o grande negócio! Pois para a existência do limite bilateral é necessário que tanto o limite lateral esquerda e o limite lateral direita devem possuir o mesmo valor. Matematicamente expressamos da seguinte forma:
lim_{x \to a}{(f(x))} = L, se somente, e se: \boxed{lim_{x \to a^+}{(f(x))} = lim_{x \to a^-}{(f(x))} = L}
Portanto, muitas vezes que seu professor, ou você que estiver estudando quiser verificar a existência de um limite, será necessário calcular os limites laterais daquela função em um determinado ponto.
Exemplo 1: Mostre que lim_{x \to 0}|x| = 0
Vamos lembrar da função modular! É importantíssimo sabermos como funciona esse tipo de função.
Uma função modular sempre retorna um valor positivo!
Portanto temos:
|x| =\begin{cases}x,\text{ se } x \geq 0 \\ -x, \text{ se } x < 0 \end{cases}O gráfico de módulo de x é que nem um bico de pato! Vejamos:
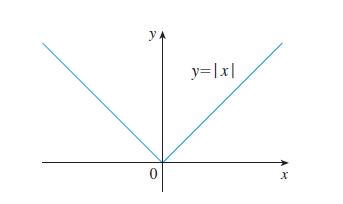
Já que queremos o lim_{x \to 0}{|x|} devemos estudar o limite dessa função quando x \to 0^+ e x \to 0^-.
Lembremos novamente que:
x \to 0^+ > 0, entrando na condição número 1 de |x|; Ou seja, |x| = x. Portanto calculando seu limite:
\boxed{lim_{x \to 0^+}{x} = 0}
x \to 0^- > 0, entrando na condição número 2 de |x|; Ou seja, |x| = -x. Portanto calculando seu limite:
\boxed{lim_{x \to 0^-}{(-x)} = 0}
Concluímos que os limites laterais são iguais! E valem 0. Portanto o limite existe e ele vale 0. Matematicamente:
\boxed{lim_{x \to 0}{|x|} = 0}
Satisfazendo então, a condição de existência de um limite
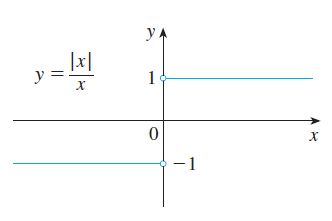
Exemplo 2: Mostre que lim_{x \to 0}{\frac{|x|}{x} não existe:}
Estudemos novamente a função modular, só que agora dividida por um determinado x!
Novamente temos que:
|x| =\begin{cases}x,\text{ se } x \geq 0 \\ -x, \text{ se } x < 0 \end{cases}x \to 0^+ > 0, entrando na condição número 1 de |x|; Ou seja, |x| = x. Portanto calculando seu limite:
\boxed{lim_{x \to 0^+}{\frac{x}{x}} = 1}
x \to 0^- > 0, entrando na condição número 2 de |x|; Ou seja, |x| = -x. Portanto calculando seu limite:
\boxed{lim_{x \to 0^-}{\frac{(-x)}{x}} = -1}Veja que qualquer coisa pode mudar na matemática! Uma divisão por x, faz o limite não existir!!
vejamos que os limites laterais são diferentes, não aceitando a condição de existência do limite. Portanto:
\boxed{lim_{x \to 0^-}{\frac{(|x|)}{x}} \ne lim_{x \to 0^+}{\frac{(|x|)}{x}}}
O limite não existe!!!!