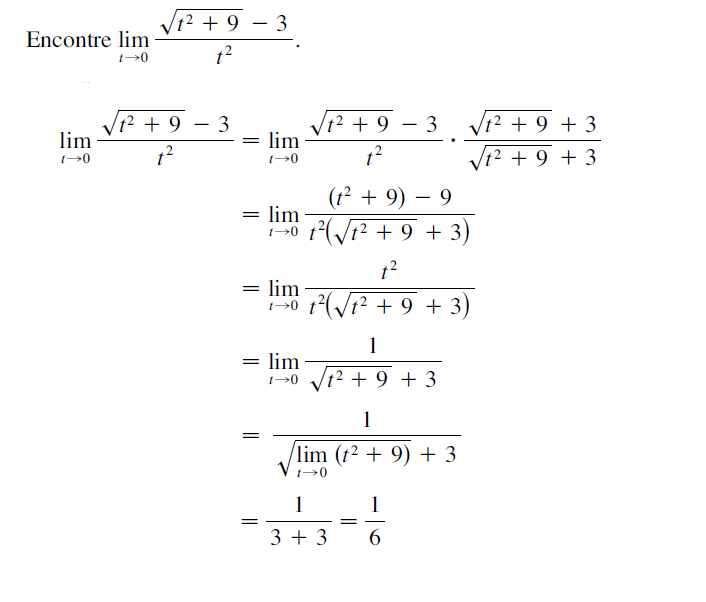Cálculos de Limites a partir da Propriedade da Substituição

Cálculos de Limites a partir da Propriedade da Substituição é a forma mais simles e básicas de se resolver um limite.

Vimos na aula anterior “propriedades dos limites” que é possível o desenvolvimento de vários cálculos a partir da álgebra de propriedades que o mesmo tem. Caso não tenha visto essa aula, é importante que veja meu caro aluno!

Agora vamos para outra propriedade dos limites, que é a mera substituição do valor que um determidado x tende diretamente para função da curva especificada. Vejamos:

Propriedade da Substituição:

Se a função f for uma função racional ou polinomial, podemos considerar que:

$\boxed{lim_{x \to a}f(x) = f(a)}$

Ou seja, imagine o seguinte:

$lim_{x \to 2}({x^2 – x + 2})$

Podemos simplesmente fazer isso:

$f(2) = (2)^2 - (2) + 2$

$\boxed{f(2) = 4}$

Quando não podemos fazer isso? Quando temos problema de indeterminação.

Problema da Indeterminação:

Um limite é indeterminado, quando substituimos os valores e o resultado fica da seguinte forma:

$i) \boxed{lim_{x \to a}{f(x)} = \frac{0}{0}}$

$ii) \boxed{lim_{x \to a}{f(x)} = \frac{\pm\infty}{ 0}}$

$iii) \boxed{lim_{x \to a}{f(x)} = \frac{ 0}{\pm\infty}}$

$iv) \boxed{lim_{x \to a}{f(x)} = \frac{\pm\infty}{\pm\infty} }$

Imagine agora:

$lim_{x \to 1}{\frac{x^2 – 1}{x – 1}}$

Assim, com a substuição direta cairíamos, na indeterminação i).

pois: $\boxed{f(1) = \frac{0}{0}} \rightarrow é um indeterminação!$

Resolvendo limites indeterminados:

Temos que recorrer as nossas ferramentas de álgebra! Ou seja, podemos apelar para fatoração de funções, ou simplificações de divisões, entre diversas outras ideias. Mostrarei muitos exeplos resolvidos sobre isso.

Exemplo 1: Calcule o limite $lim_{x \to 1}{\frac{x^2 – 1}{x – 1}}$ :

Resposta: Podemos fatorar o numerador da expressão.

Fatorando função quadrática:

i) Encontre as raízes da função. f(x) = 0.

$x^2 – 1 = 0 \rightarrow x^2 = 1$

$\boxed{x = \sqrt{ 1} = \pm 1}$

ii) expresse a equação de segundo grau da seguinte forma:

$ax^2 + bx + c = a*(x - x_0)*(x - x_1)$

Onde:

x_0 e x_1 são as raízes do função quadrática.

Portanto podemos simplesmente expressar:

x^2 - 1 = 1*(x + 1)*(x - 1)

veja que se você fazer a distributiva volta a ser a mesma coisa!

Portanto nosso limite fica da seguinte forma.

$lim_{x \to 1}{\frac{(x + 1)*(x – 1)}{x – 1}}$

$lim_{x \to 1}{\frac{(x + 1)*\cancel{(x – 1)}}{\cancel{x – 1}}} = lim_{x \to 1}(x + 1)$

Agora basta substituir denovo:

$\boxed{lim_{x \to 1}(x + 1) = (1 + 1) = 2}$

Exemplo 2:

Resolva os exercícios a) e b) justificando as passagens dos cálculos:

a) $lim_{x \to 5}{(2x^2 – 3x + 4)}$

lim_{x \to 5}2x^2  –  lim_{x \to 5}3x  +  lim_{x \to 5}4

Pelas propriedades algebricas chegamos a seguinte situação:

2*lim_{x \to 5}x^2  –  3*lim_{x \to 5}x  +  lim_{x \to 5}(4)

Fazendo a substituição nas funções temos:

$\boxed{2*(5)^2 – 3*(5) + 4 = 50 – 15 + 1 = 36}$

b) $lim_{x \to -2}{[\frac{x^3 + 2x^2 – 1}{5 – 3x}}]$

Pelas propriedades dos limites chegamos na seguinte relação:

$\frac{lim_{x \to -2}(x^3) + 2lim_{x \to -2}{(x^2)} – lim_{x \to -2}(-1)}{lim_{x \to -2}(5) – lim_{x \to -2}(3x)}$

Substituindo valores temos:

$\boxed{\frac{(-2)^3 + 2(2^{-2}) – 1}{5 – (3*(-2))} = \frac{-1}{ 11}}$

Exemplo 3: Resolva o limite de uma função definida em partes

Encontre o $lim_{x \to 1}[g(x)]$ , onde g(x) é definido como:

$g(x)=\begin{cases}x+1,\text{ se } x \ne 0 \\ \pi, \text{ se } x = 1 \end{cases}$

Uma função por partes tem diferentes comportamentos dada uma condição em seu domínio. Nesse caso vemos que g(x) = x+1 quando x é diferente de 0 e igual a pi quando x = 1. Podemos representar o gráfico abaixo da seguinte forma:

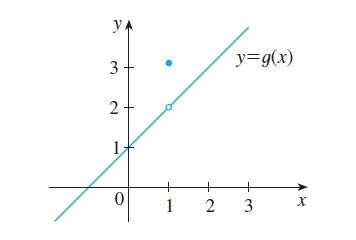
Lembre-se das aulas anteriores que o limite pode ser calculado, mesmo que o ponto definido(“escuro”) esteja em outro valor de g(x). Ou seja:

Quando $x \to 1 \ne x = 1$ — lembre-se disso!

Portanto quando calculamos o limite de g(x) quando x tende a 1, é diferente de quando x efetivamente vale 1. De modo a chegarmos na seguinte relação:

$\boxed{lim_{x \to 1^+}{g(x)} = lim_{x \to 1^+}{(x + 1)} = 2}$

$\boxed{lim_{x \to 1^-}{g(x)} = lim_{x \to 1^+}{(x + 1)} = 2}$

$\boxed{lim_{x \to 1}{g(x)} = lim_{x \to 1^+}{(x + 1)} = 2}$

eeeeeee, presta atenção que:

$\boxed{g(1) = \pi}$

Exemplo 4:

Calcule: $lim_{h \to 0}{\frac{(3 + h)^2 – 9}{h}}$

Se utilizarmos a propriedade da substituição direta acontecera o seguinte:

$lim_{h \to 0}{\frac{(3 + h)^2 – 9}{h}} = \frac{(3 + 0)^2 – 9}{0} = \frac{0}{0}$

Uma indeterminação! Temos que apelar para álgebra.

Portanto, se abrirmos o produto notável (3 + h)² chegamos à seguinte expressão:

lim_{h \to 0}{\frac{((3)^2  +  2*3*h  +  h^2)  –  9}{h}} =  lim_{h \to 0} \frac{(9  + 6h  + h^2  -9)}{h} =  lim_{h \to 0} \frac{(\cancel{9}  + 6h  + h^2  \cancel{-9})}{h} = lim_{h \to 0}{\frac{h^2  +  6h}{h}}

Deixando h em evidência temos que:

lim_{h \to 0}{\frac{h*(h  +  6)}{h}}

lim_{h \to 0}{\frac{\cancel{h}*(h  +  6)}{\cancel{h}}}

$\boxed{lim_{h \to 0}{(h + 6)} = (0 + 6) = 6}$

Exemplo 5:

Veja no exemplo 5 temos uma raíz no numerador. E para tirarmos essa raíz temos que multiplicar pelo conjugado. Farei um vídeo explicando cada caso de limite e como podemos resolve-los. Por enquanto entenda que se multiplicarmos pelo conjugado emcima e embaixo podemos simplificar o limite e tirarmos da situação de indeterminação.