Conteúdos Sugeridos e Recomendados para o artigo: Derivadas de Funções Implícitas

• Funções
• Regra da Cadeia
• Derivadas de Funções Trigonométricas

Definição de funções implícitas:

Funções implícitas são aquelas nas quais a relação entre as variáveis não está explicitamente resolvida para uma variável em termos da outra(s). A função não está explicitamente no formato y = f(x) , é necessário que aja uma manipulação algebrica para torna-la uma função explícita.

Como exemplo temos o círculo unitário uma função implícita:

x^2 + y^2 = 1

Não é possível visualizar que essa equação pode ser expressa na forma y = f(x). Manipulando algebricamente a equação acima:

y^2 = 1 - x^2

Tirando a raiz da equação podemos visualizar uma função explícita. Veja o formato abaixo.

y = \pm \sqrt{1-x^2}

Exemplo 1 : (Guidorrizi – 2002)¹ – Determine uma função que seja dada implicitamente pela equação y^2 + xy - 1 = 0.

A função dada no exemplo é implícita. Não podemos visualizar de primeira a função na forma y = f(x). Se considerarmos y a variável de interesse e x como uma constante, temos uma equação de segundo grau. Vejamos:

1.{\color{red}{y}^2} + x{\color{red}{y}} - 1 = 0

A equação de segundo grau é expressa na sua forma geral: ay^2 + by + c, \therefore a = 1, b = x e c = -1

\Delta = x^2 - 4(1)(-1) = x^2 + 4

A função na sua forma explicita fica:

\boxed{y = \frac{-x \pm \sqrt{x^2 + 4}}{2}}

Derivadas de Funções Implícitas – Métodos:

Considerando o exemplo acima, podemos já prever que derivar uma função implicita pode ser realizada de maneiras diferentes. Eu listo aqui duas formas:

Método 1: Manipular equação e depois derivar.

1. Transformar a função implícita para explícita
2. Aplicar um método de derivação da função explícita y = f(x)

Método 2: Método da derivação implícita

1. Derivar ambos os lados da equação
2. Aplicação da regra da cadeia na variável dependente (Geralmente é o y)
3. Isolar y’, assim descobriremos sua derivada.
4. Não se preoucupe, vamos fazer na prática e ficará mais claro, não pare aqui, vá em frente!

Derivando Funções Implicitas:

A derivação implícita permite derivar equações onde variáveis se relacionam de maneira complexa. É possível aplicar essa técnica em diversos cenários, desde problemas geométricos até modelos matemáticos mais abstratos.

Para dominar a derivação implícita, é elementar ter conhecimento sobre a regra da cadeia e praticar com diferentes tipos de funções implícitas.

Seguindo o método 2, vamos resolver alguns exercícios.

Derivação Implícita de um Círculo Unitário:

O círculo unitário é dado pela seguinte função:

x^2 + y^2 = 1

Passo 1: Derivar ambos os lados da igualdade.

\frac{d}{dx}(x^2 + y^2) =\frac{d}{dx}(1)

Passo 2: Aplicação da regra da cadeia na variável dependente (Geralmente é o y)

2x + 2yy' = 0

Veja que o y' = \frac{dy}{dx} que é exatamente a derivada da função que estamos interessados. Desse modo vamos ao passo 3: Isolar y’.

2x = -2y\frac{dy}{dx}

\therefore \boxed{\frac{dy}{dx} = -\frac{x}{y}}

A derivada y’ representa a inclinação da tangente ao círculo em qualquer ponto (x, y) da curva. Essa inclinação depende tanto da coordenada x quanto da coordenada y. Veja na próxima questão.

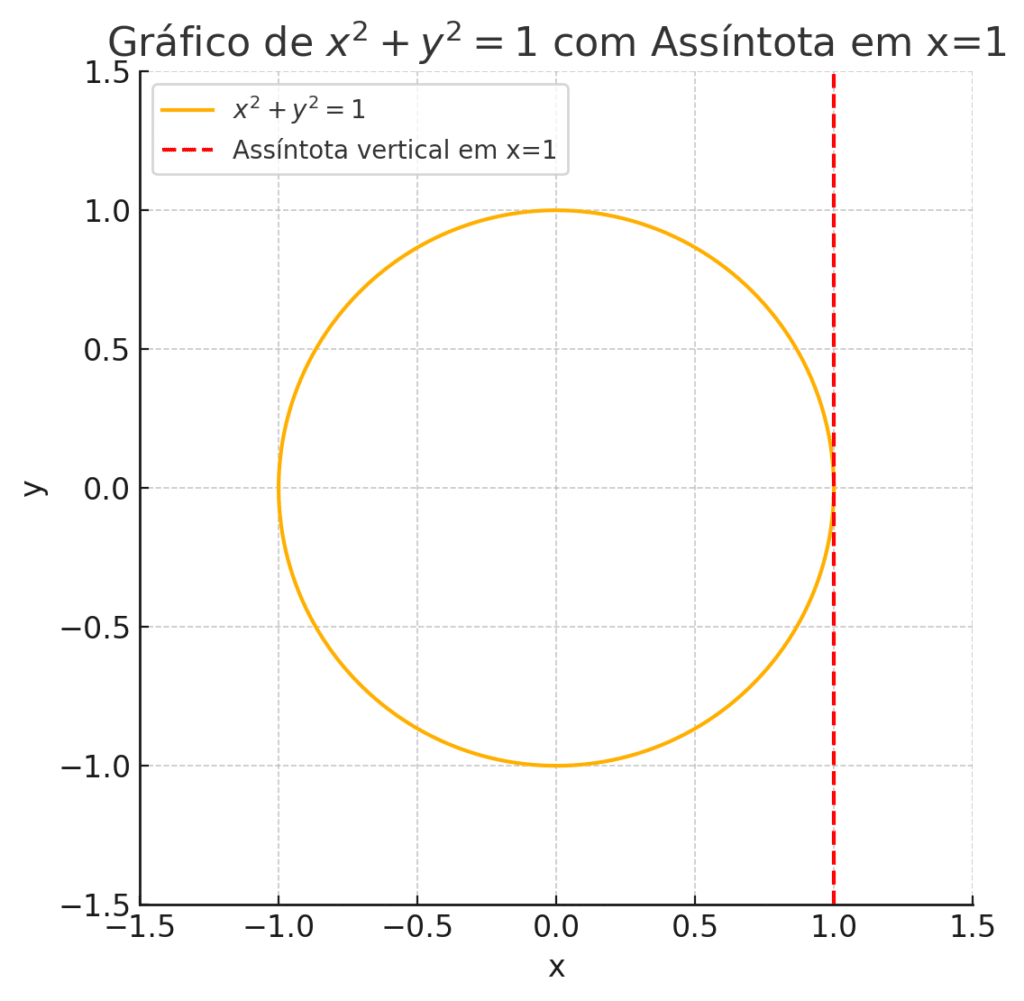
Encontre uma equação da reta tangente ao círculo unitário no ponto (1,0):

A equação da reta tangente tem a seguinte configuração: (“yoyo mixxo”)

y - y_0 = \frac{dy}{dx}(x - x_0)

Nesse caso:

y - 0 = \left[lim_{x\rightarrow0}\left(\frac{-1}{0}\right)\right](1 -0)

y = \mp\infty

Temos uma assíntota vertical no ponto (1,0). Pode ser traçado por um lápis e uma caneta. Convido você viver essa experiência de desenhar um círculo unitário e desenhar uma reta que tangencia o ponto (1,0) e você vai ver com seus próprios olhos como a reta funciona.

(James Stwert² – 7ª Edição) Encontre y’

sen(x+y) = y^2cos(x)

Antes de mais nada, tente resolver esse exercício sozinho. Aplicar os 3 passos acima é a base para resolver esse exercício.

Vamos lá. Passo 1: Derivar ambos os lados da equação

[sen(x+y)]' = [y^2cos(x)]'

Passo 2: Aplicação da regra da cadeia na variável dependente (Geralmente é o y)

Atenção nos seguintes detalhes. Do lado esquerdo da equação temos uma função composta no qual é derivada pelo método da regra da cadeia. (Cor verde)

Noutro lado temos o produto de duas diferentes funções, portanto aplica-se a regra do produto para obter sua derivada, e ainda há uma função composta com y, aplicando-se a regra da cadeia novamente. (Cor azul).

cos(x+y). {\color{green}{(x+y)'}} = \color{blue}{2yy'.cos(x) -y^2sen(x)}

cos(x+y)(1 + y') = 2yy'cos(x) - y^2sen(x)

Passo 3: Isolar y’. Dessa maneira é preciso deixar todos os y’ de um lado da equação, deixar tudo em envidência e isolá-lo.

y' cos(x+y) -2yy'cos(x)=-y^2sen(x) - cos(x+y) 

y'(cos(x+y) -2y.cos(x))=-y^2sen(x) - cos(x+y) 

y' = \frac{-y^2sen(x) - cos(x+y) }{cos(x+y) -2y.cos(x)}

Trabalhando com os sinais temos a seguinte resposta:

\boxed{y' = \frac{y^2sen(x) + cos(x+y) }{2y.cos(x) - cos(x+y)}}

Lembre-se sempre que além de toda essa álgebra, há inúmeros significados para esse troço acima de nós! Independênte do tamanho do resultado, uma derivada sempre carregará consigo mesmo suas próprias características. Convido você relembrar o que é uma derivada no sentido físico e geométrico.

Por Que Usar Derivação Implícita?

A derivação implícita é especialmente útil em situações onde:

• As variáveis estão intrinsecamente relacionadas e não podem ser facilmente isoladas.
• A função implícita descreve formas geométricas complexas, como elipses, hipérboles ou curvas que não possuem fórmulas explícitas simples.
• Utilizamos a derivação inversa para resolver derivadas de funções trigonométricas inversas

Veja a aula de derivação implicita de funções trigonométricas inversas.

Referências:

1. Guidorizzi, H. L., Um curso de Cálculo, V. 1, Livros Técnicos e Científicos Ed. Ltda, 5 ^a edição (2001).
2. STEWART, James. Cálculo, Volume 1. 7. ed. São Paulo: Cengage Learning, 2013.