Introdução:
Vimos anteriormente que o aumento da temperatura de um material significa que as moléculas que compõe o mesmo ganham mais movimento e velocidade. A agitação é causada pelo aumento das distâncias médias entre as moléculas, o que tem como consequência A expansão do material.
Intuitivamente temos que a diminuição da temperatura leva a menores distâncias médias entre as moléculas, tal que, é a causa da contração do material.
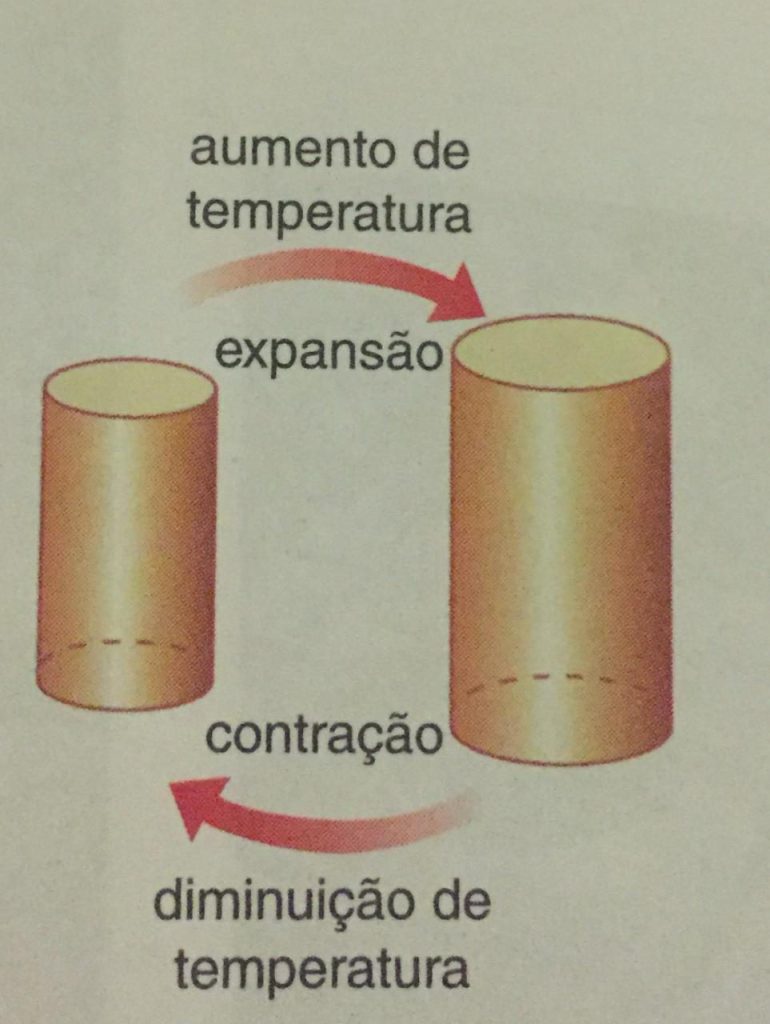
A olho nu, é realmente muito difícil enxergar a varição do tamanho do material a partir da variação de temperatura dele. Para você ter noção: A variação de temperatura em uma barra de metal de 1m de 0ºC para 100ºC da uma variação de 1mm de comprimento!
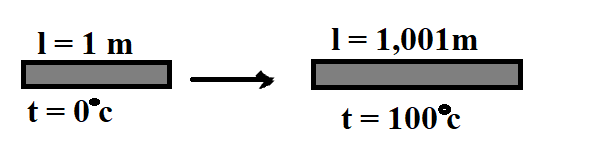
Dilatação linear dos sólidos:
Nosso objetivo é de conseguir calcular a expansão ou contração de um corpo a partir da variação de temperatura que ele tem. Além disso, nesse tópico vamos focar na mudança de tamanho de apenas uma dimensão geométrica, o que chamamos de dilatação linear.
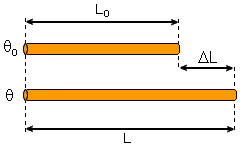
Consideremos um barra que tenha o comprimento de Lo à temperatura de θo e o comprimento L à temperatura de θ. As variações de comprimento e temperatura são dados por:
(1) ΔL = L- Lo
(2) Δθ = θ – θo
Para calcularmos a variação de comprimento que uma barra sofre a partir da variação de temperatura usamos a seguinte fórmula:
(3) ΔL = α.Lo.Δθ
Onde:
ΔL = Variação de comprimento da barra
α = Coeficiente de proporcionalidade (dado pelo tipo de material)
Lo = Comprimento da barra à temperatura θo
Δθ = Variação de temperatura sofrida pela barra
Podemos também transformar a equação 3 por:
- ΔL = α.Lo.Δθ
- L – Lo=α.Lo.Δθ
- L=Lo+α.Lo.Δθ
- L = Lo(1+α.Δθ) Podemos usar essa fórmula também!
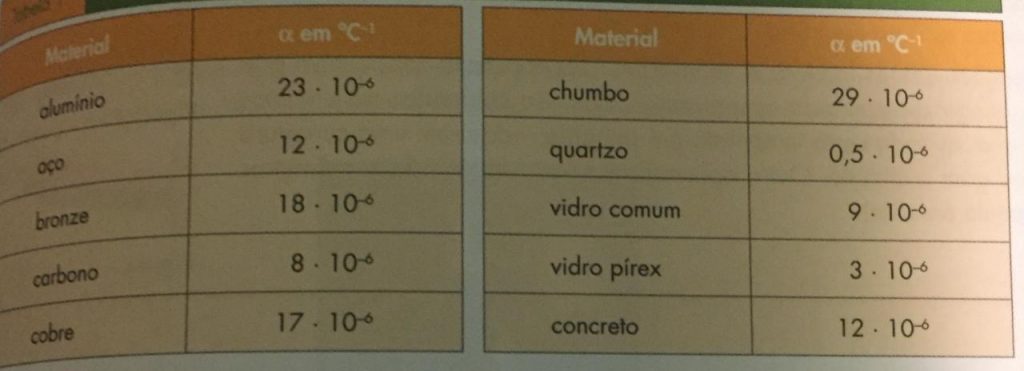
tabela dos coeficientes de proporcionalidade linear:
Unidade do coeficiente de proporcionalidade:
Portanto temos que: α= ΔL / Lo.Δθ
Trocando todas as variáveis por unidades do SI temos:
α = [m] / [m].[ºC]
–>As unidades são: α= [ºC]-1
Lâmina bimetálica:
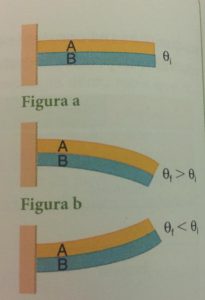
É bom reconsiderarmos que quanto maior o coeficiente de proporcionalidade α de um corpo, maior a capacidade de dilatação ele tem a partir da variação da temperatura. Considerando uma lâmina bimetálica (figura a).
Considerando que αA>αB então significa que a lamina A contrairá ou expandirá mais que a lâmina B quando ouver variação de temperatura (Δθ). Consideremos também que as duas lâminas estão em uma temperatura inicial θo. Podem ter dois acontecimentos com a temperatura:
O sistema pode esquentar (θ>θo):
Siginifica que a lâmina A terá uma expansão maior que a lâmina B, tendo como produto final a figura b.
O sistema pode esfriar(θ<θo):
Significa que a lâmina A terá uma contração maior que a lâmina B, tal que o produto final será a figura C.
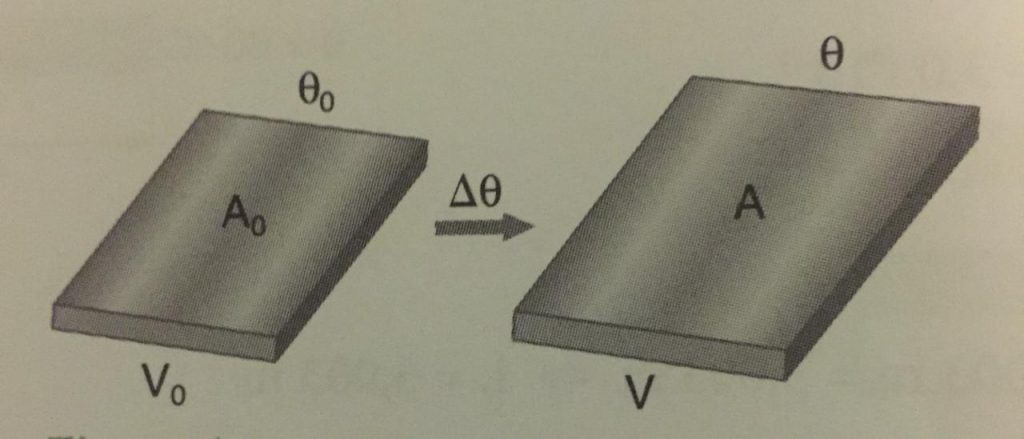
Dilatação Superficial e Volumétrica:
Diferente da dilatação linear falado um pouco acima, agora estamos falando sobre uma dilatação bidimensional ou tridimensional, ou seja, estamos falando de mais de uma dimensão. A dilatação(seja ela contração ou expansão do material) é calculado de forma diferente do que visto anteriormente, na verdade mudamos poucas coisas.
α = α
β = 2.α
γ = 3.α
Dilatação superficial (β):
ΔA = β.Ao.Δθ
ΔA = variação da área (A – Ao)
β = coeficiente de proporcionalidade superficial
Ao = Aréa à temperatura θo
Δθ = Variação de temperatura do corpo
Dilatação volumétrica (γ):
ΔV = γ.Vo.Δθ
ΔV = variação do volume (V – Vo)
γ = Coeficiente de dilatação volumétrica
Vo = Volume a temperatura θo
Δθ = Variação da temperatura do corpo
Dilatação dos líquidos:
- Os líquidos não possuem forma, eles geralmente se adaptam de acordo com o formato do recipiente.
- Quando falamos de líquidos, intuitivamente pensamos em volume, e a sua dilatação é volumétrica.
- Observe a tabela dos coeficientes de proporcionalidade dos líquidos: