Considerações Iniciais:
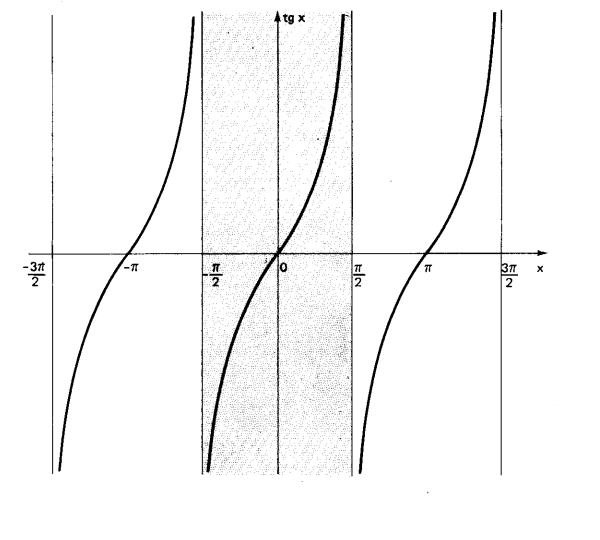
A circunferência é divida em 4 partes, sendo que cada uma delas é chamado de quadrante. A ordem dos quadrantes andam no sentido anti horário.
- Primeiro quadrante(IQ): x pertence ao IQ, se somente se satisfazer: 0+2πk ≤ x ≤ π/2+2πk
- Segundo quadrante(IIQ): x pertence ao IIQ, se somente se satisfazer: π/2+2πk ≤ x ≤ π +2πk
- Terceiro quadrante(IIIQ): x pertence ao IIIQ, se somente se satisfazer: π+2πk ≤ x ≤ 2π/3 +2πk
- Quarto quadrante(IVQ): x pertence ao IVQ, se somente se satisfazer: 2π/3+2πk ≤ x ≤ 2π +2πk
1) Função seno:
Definição:
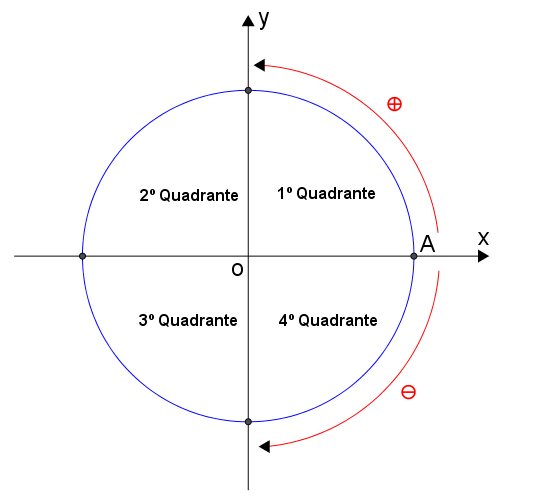
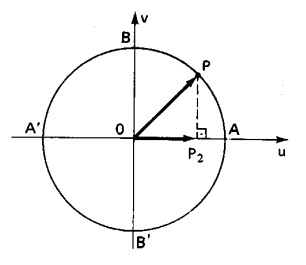
Dado x pertencente aos números reais, e seja P a imagem no ciclo, denominamos senx, a linha OP1 da imagem:
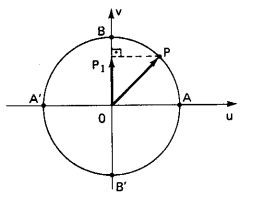
Denominamos f(x)=senx
Propriedades da função seno:
- A imagem de f(x) é de [-1,1] ou seja seno varia de -1 a 1.
- Os valores em que senx ≥ 0 se encontram no IQ e IIQ.
- Os valores em que senx ≤ 0 se encontram no IIIQ e IVQ.
- Seno é um ciclo, tal que seu periodo é dado por 2π.
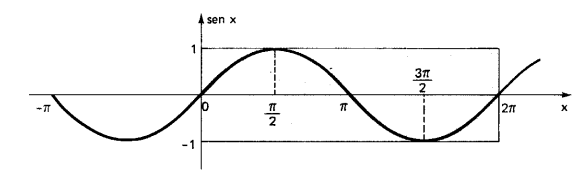
Essas propriedades vão ficar mais claras quando você ver o gráfico de seno, conhecido como senoide:
2) Função cosseno:
Definição:
Indicamos cosx como a abssiça OP2 em relação ao sistema uOv.
Propriedades de cosx:
- A imagem de cosseno varia de -1 a 1.
- Para valores de cosx ≥ 0 se x pertencer ao IQ ou IVQ.
- Para valores de cosx ≤ 0 se x pertencer ao IIQ ou IIIQ.
- Cosx é uma função periódica, uma vez que é um ciclo e seu período é dado por 2π.
Análise tais propriedades no gráfico de cosseno, chamado de cossenóide:
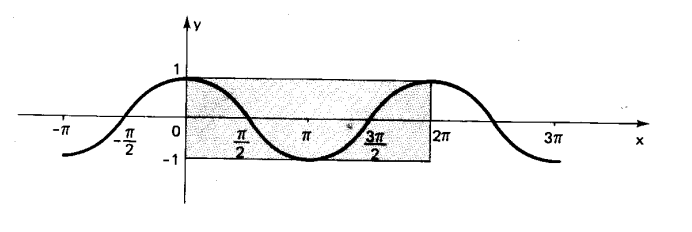
3) Função tangente:
Para função tangente, devemos considerar todo x ≠ π/2 + 2πk, uma vez que tanx com x pertencente a esses valores não existe!
Denominamos a tangente como a intersecção de OP e AT. tal que o falor de f(x) = tanx = AT.
Observe a figura abaixo:
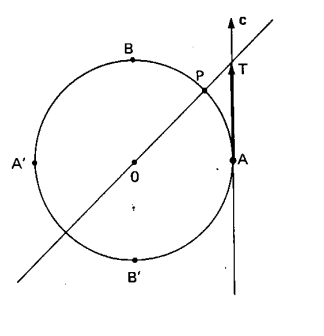
Propriedades:
- O domínio de tanx é para todo x ∈ ℜ, x = ≠ π/2 + 2πk
- Se x pertence ao domínio, valores de Y será real.
- Para tanx > 0, x pertence aos quadrantes I e III.
- Para tanx < 0, x pertence aos quadrantes II e IV
- tanx é uma função periódica, tal que o período é π.
- Os valores dos quadrantes se identificam, tal que: tan(x+kπ) = tanx
Gráfico: