1) Introdução:
As funções quadráticas são aquelas possui em pelo menos uma de suas parcelas uma variável dependente elevado ao quadrado. Observe que a potência máxima dessa variável dependente é 2 – por isso – Função Polinomial de 2º grau. Ela é generalizada com a seguinte formula: f(x) = ax2 + bx + c.
Definição:
Seja uma função f:ℜ -> ℜ, chama-se quadrática quando existem números reais a,b,c com a ≠ 0, tal que:
f(x) = ax2 + bx + c. Para todo x pertencente aos reais.
2) Cálculo dos Valores de f(x) correspondentes a um x:
Assim como calculamos o valor de qualquer função, basta substituir o valor x em f(x).
Considerando a função quadrática f(x) = 3x2 – 4x + 1 :
Calculando f(x) para valores de:
x =1: f(1) = 3.(1)2 – 4(1) + 1 = 0
x = 2; f(2) = 3.(2)2 – 4.(2) + 1 = 5
x = 0; f(0) = 3.(0)2 – 4.(0) + 1 = 1
x = √2 ; f(0) = 3.(√2)2 – 4.(√2) + 1 = 7 – 4√2
3) Raízes de uma Função Quadrática:
Podemos chamar as raízes de uma equação quadrática como o zero da função. Ou seja quando f(x) = 0. E o que isso significa? Significa que estamos encontrando valores de x para que f(x) = 0. Em gráficos são os valores de x em que f(x) cruza o eixo x (y = 0). Basicamente igualamos f(x) = 0, e fazemos delta e Bhaskara para descobrirmos (se existir) as raízes da função.
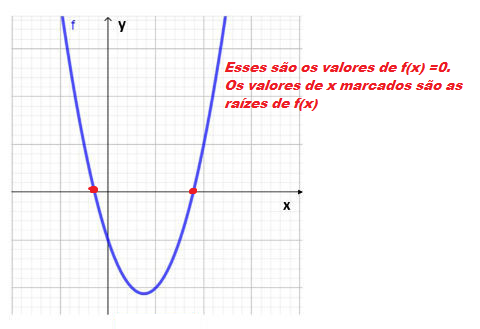
A raízes de f(x) são os valores de x quando f(x) = 0, certo?
Portanto f(x) = 0.
x2 – 4 = 0 -> x2 = 4 ; Tirando a raíz quadrada dos dois lados temos:
√(x2) = √(4) -> x = ±2
Concluí-se que para x =-2 e x= +2 os valores de f(x) = 0. Então esses valores de x são as raízes de f(x).
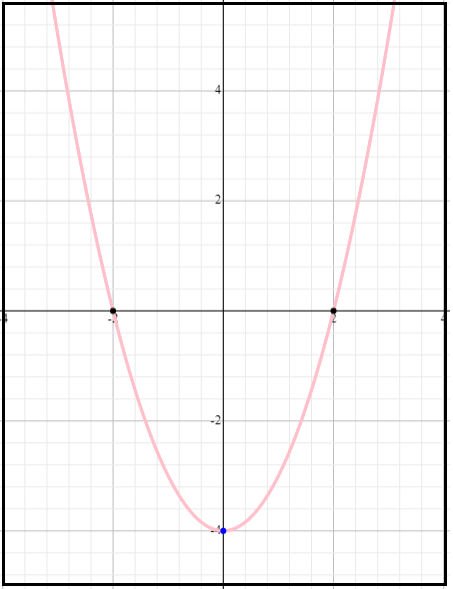
4) Gráficos de função de 2º Grau:
Primeiramente uma função de segundo grau é uma Parábola!
Veja fotos de parábolas:
Reflexão: Uma antena “parabólica” é chamada assim por causa do seu formato de parábola.


Eu poderia me estender falando sobre as parábolas e como elas se comportam, da onde se originalizaram e muito mais. Porém como o objetivo é ensinar como traçar esse tipo de gráfico. Além disso quero discutir sobre os vértices de uma função de segundo grau e como podemos interpreta-las na vida real.
4.1) Construindo Gráfico de f(x):
Vamos fazer o gráfico da forma mais simples possível. Primeiramente pegamos f(x) e calculamos seus valores para valores de x. Depois marcamos os pontos no sistema de coordenadas Oxy. E depois tentamos traçar uma parábola.
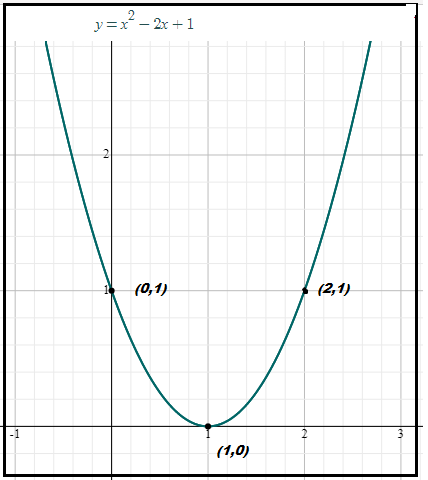
Construa o gráfico de f(x) = x2 -2x + 1
Para x = 0; f(0) = (0)2 -2.(0) + 1 = 1
Para x = 1; f(1) = (-1)2 -2(1) + 1 = 0 (x =0 é raíz da função f)
Para x =2; f(2) =(2)2 -2(2) + 1 = 1
Observe o gráfico ao lado e olhe os pontos marcados e o desenho da parábola.
4.2) Como que os parâmetros "a, b, c" Interferem no Gráfico:
Esse ponto da matéria é importantíssimo! Preste atenção como os valores de a b e c transformam o gráfico.
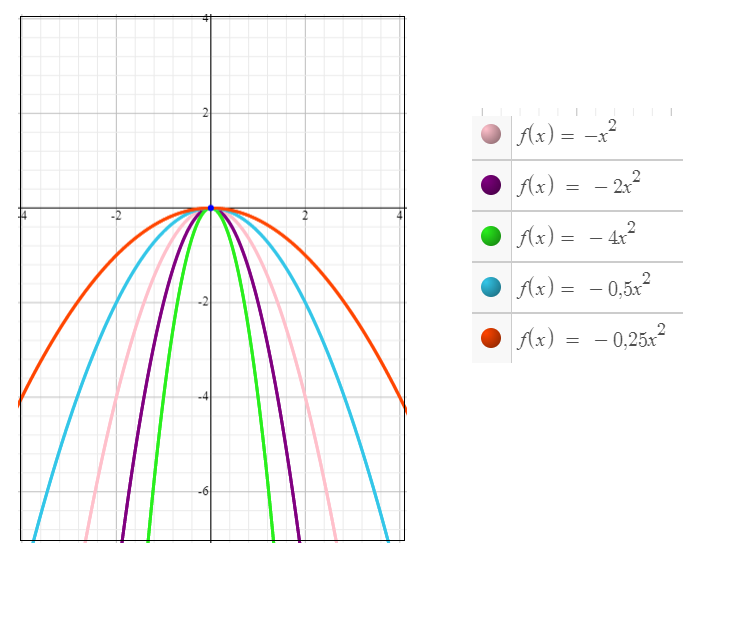
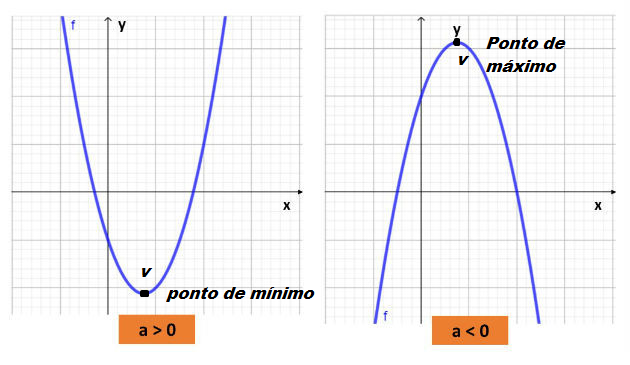
1) O sinal de a é responsável pela concavidade do gráfico. Para a>0 a concavidade é para cima e para a<0 a concavidade é para baixo.
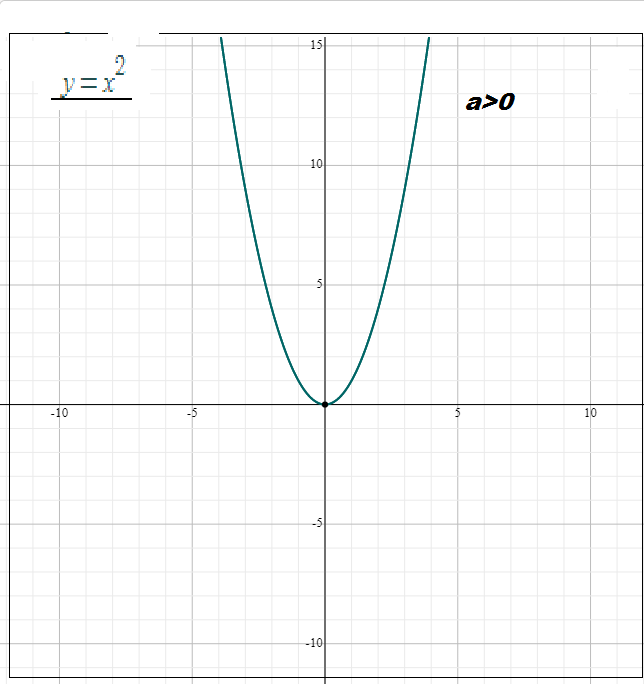
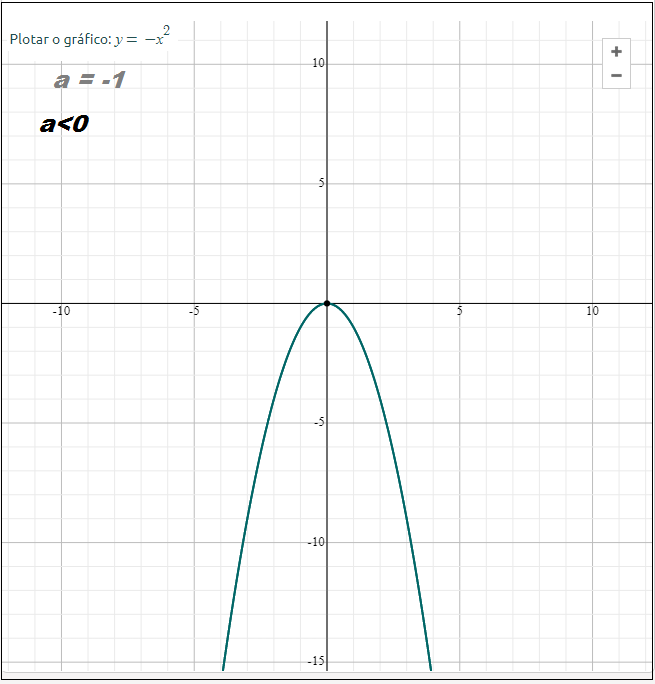
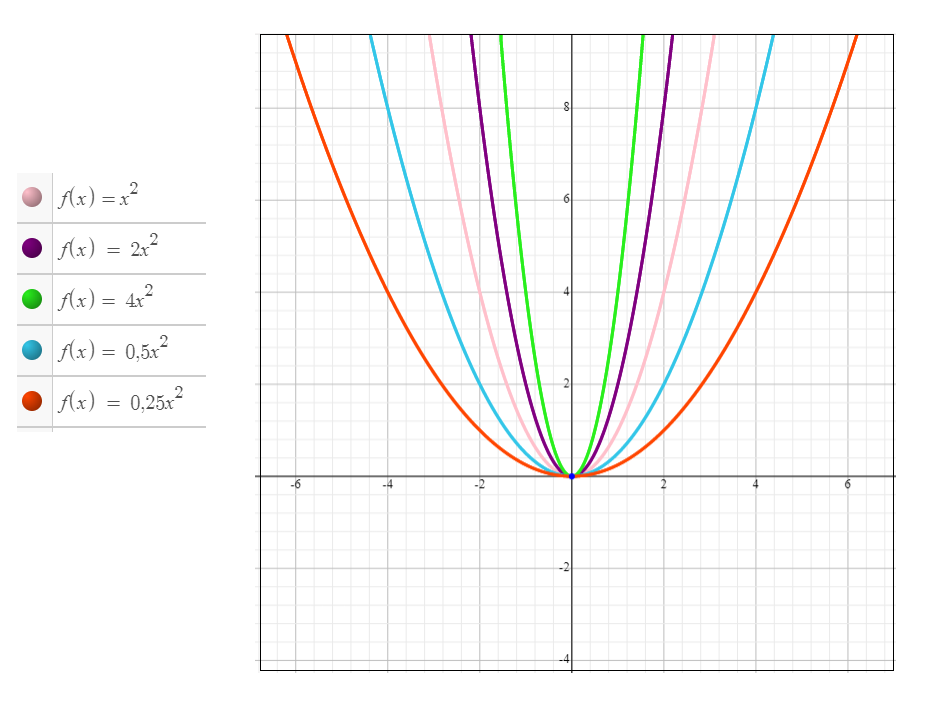
2) Enquanto maior o valor de a, menor será a abertura do gráfico:
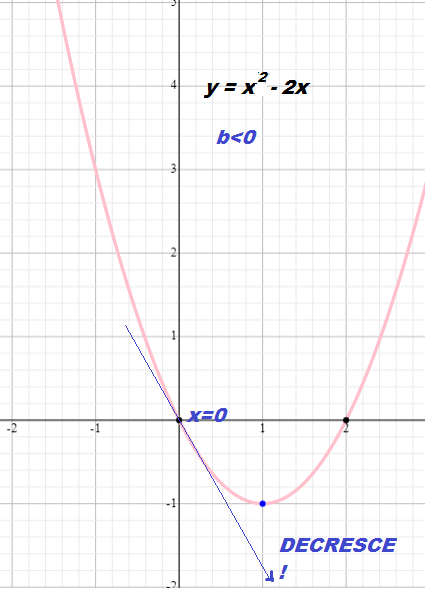
3) O parâmetro b já é um pouco mais complexo, mas de forma bem abrangente, dizemos que o sinal de b nos indica se o gráfico é crescente ou decrescente no ponto x =0.
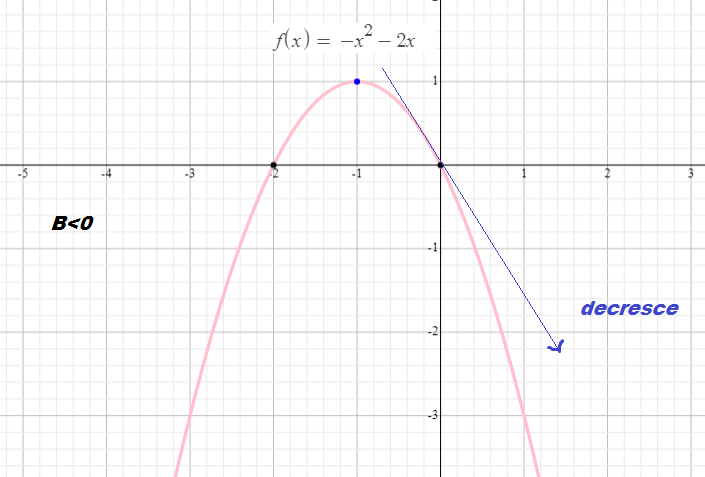
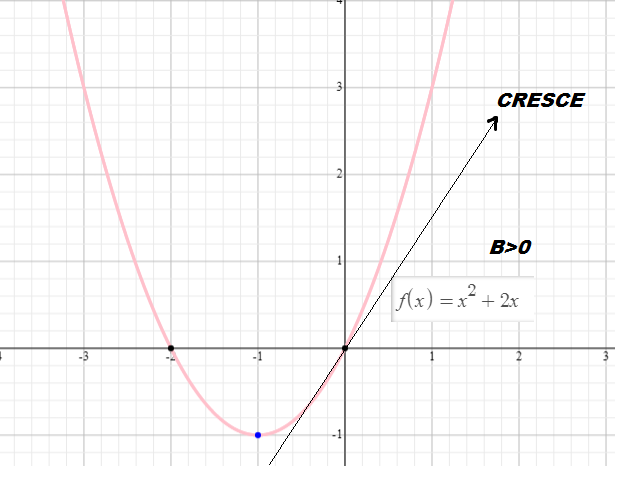
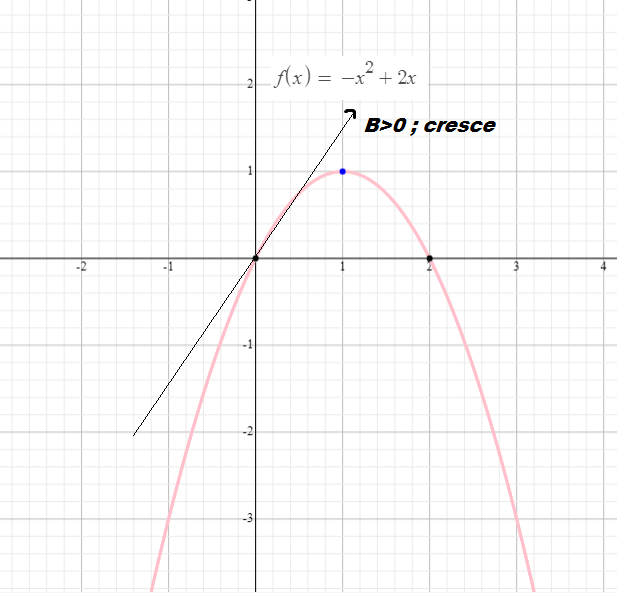
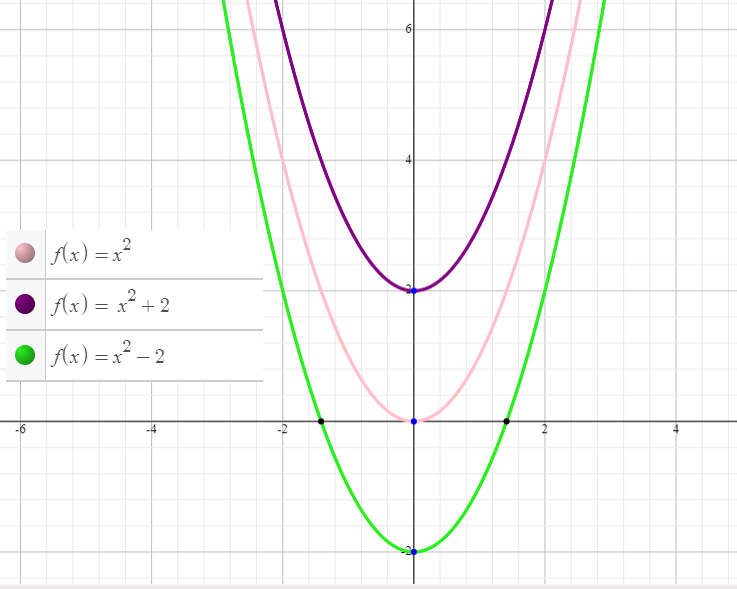
4) O parâmetro c indica o ponto de y quando x=0. Ou seja onde corta o eixo y .
Algebricamente podemos mostrar onde a função vai cortar o eixo y. Uma vez que o ponto de “corte” no eixo y é quando x =0.
A função desenhada me rosa f(x) = x2 e portanto f(0) = 0.
A função desenhada de roxo: f(x) = x2 + 2 e portanto f(0)=2.
A função desenhada em verde claro: f(x) = x2 – 2 portanto f(0) = -2
Observe onde os pontos estão no eixo y. São esses pontos calculados.
4.3) Vértice de uma Parábola:
O vértice de uma parábola é a “ponta” do gráfico. E essa ponta é representada por um único ponto (x,y). Esse ponto pode nos indicar o valor máximo ou valor mínimo da parábola tudo depende do sinal do parâmetro a. Por que?
Pois para a > 0 , a concavidade é para cima e então o vértice do gráfico é para baixo – então seu ponto de mínimo. Para a<0, a concavidade é para baixo, logo seu vértice é para cima – portanto seu ponto de máximo.
Se temos f(x) = ax2 + bx + c podemos calcular seu vertice da seguinte maneira:
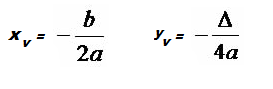
Lembrando que: Δ = b2 – 4.a.c
Qual são as importâncias de encontrar o vértice de uma parábola?
- Podemos usar isso como um complemento para construir o gráfico de f(x).
- É o ponto de máximo ou mínimo do gráfico – ou seja – podemos interpretar esses pontos de uma forma aplicada ao mundo real.
a) Qual é a altura máxima alcançada pelo foguete?
b) Em que instante t o foguete alcançou sua altura máxima?
c) Esboce o gráfico da função para t>0, identifique os pontos no qual h(t) =0 e t =0. Além isso, exiba o vértice do gráfico e mostre que esse vértice representa a altura máxima alcançada no instante t segundos.
d) Explique a importância do vértice nesse tipo de problema.
Como dito antes, temos uma função de segundo grau, no qual: a = -2, b = 50, c =0. Já que a < 0, temos uma parábola com concavidade para baixo e então um ponto de máximo representado pelo vértice dessa parábola. b = 50t, significa que em t = 0 temos uma função crescente. E c = 0, quer dizer que o gráfico cruza o eixo y com y=0. A função é dada como h(t), logo os pontos serão representados por (t,h(t)).


Se você chegou até aqui, parabéns! “Temos ser que nem uma formiga, passos pequenos e sempre em frente.”
Próximas aulas vamos fazer inúmeros exercícios em busca te praticar toda a teoria de funções e assim podemos dar o próximo passo que são as funções modulares!