1. Introdução:
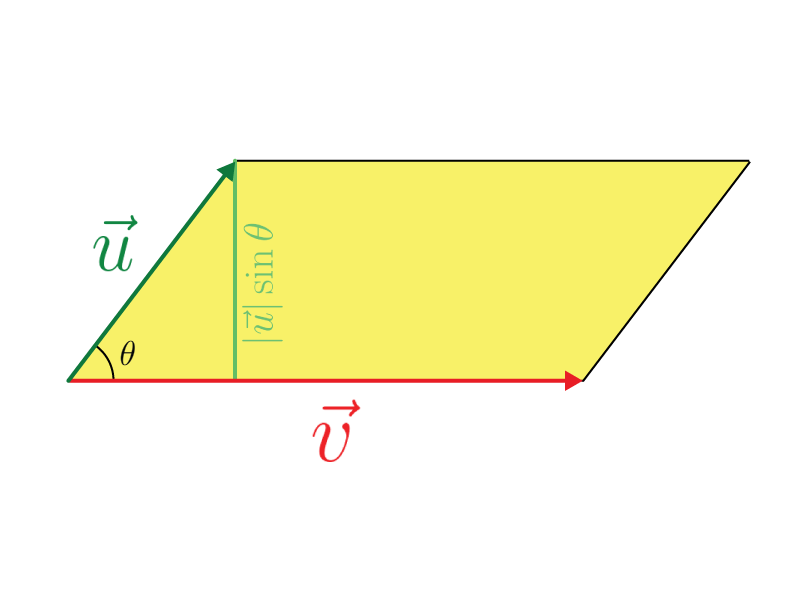
Podemos usar integrais duplas para calcula a área de dada uma superfície z = f(x,y). Usaremos para definir tal área o recurso de Geometria Analítica – que é o produto vetorial – Pois o seu módulo é a área do paralelogramo gerado por dois vetores.
2. Definindo a área de uma superfície:
Seja S uma superfície no qual é dado por z = f(x,y), onde f possui derivadas parciais contínuas. Vamos inicialmente considerar que z = f(x,y) está definida em um domínio retangular.
Assim como a maioria dos métodos anteriores para calcularmos volumes e áreas, vamos subdividir o domínio retangular em vários mini retângulos. Ou seja partiremos o valor de x em m partes iguais e o valor de y em n partes iguais. dizemos então que a base do retângulo é dado por Δx e a altura do retângulo como Δy.
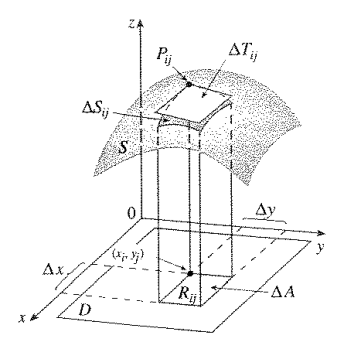
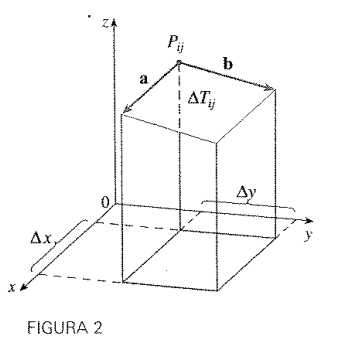
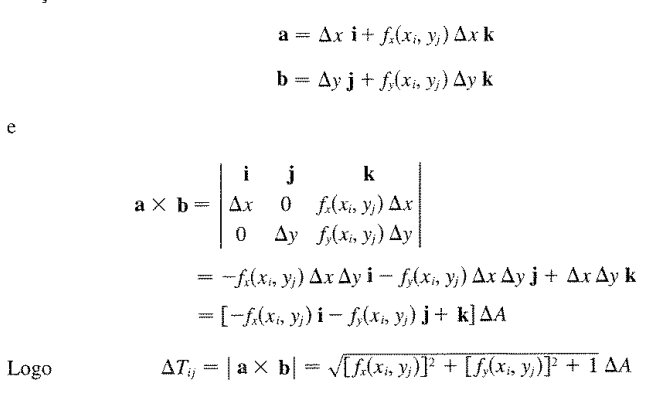
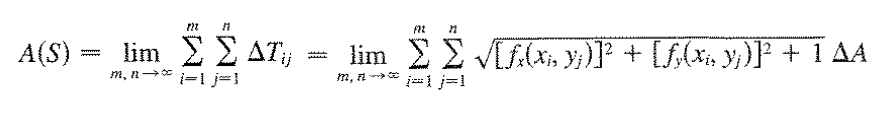
Pela definição de Integrais duplas, podemos então expressar a Área da superfície como:
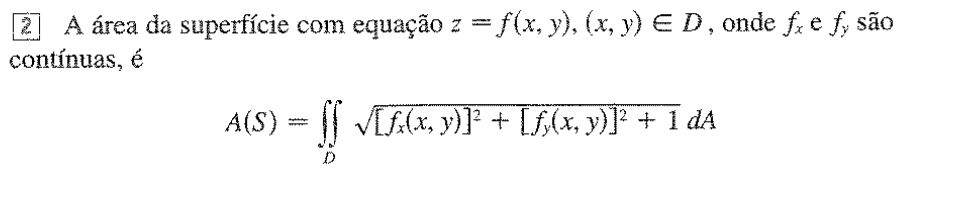
Podemos expressar as derivadas de outra forma:
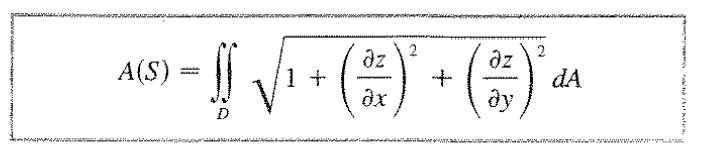
Exemplos Resolvidos:






