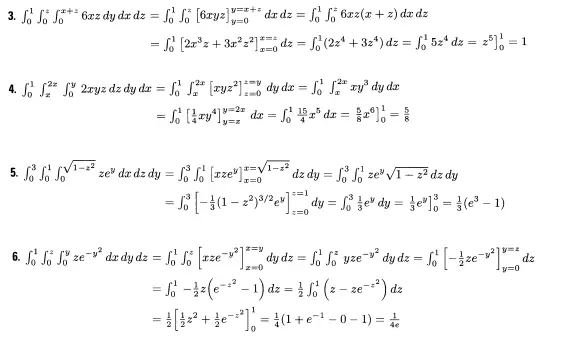1. Definição:
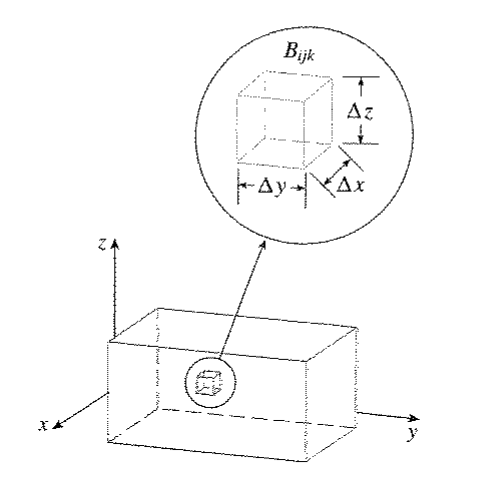
Definimos integral de uma variável em uma curva, integral de duas variáveis em um sólido definido em Oxy e agora vamos definir a integral tripla em um cubo (Oxyz). Se você entendeu as integrais simples e duplas, as integrais triplas não vou te surpreender!
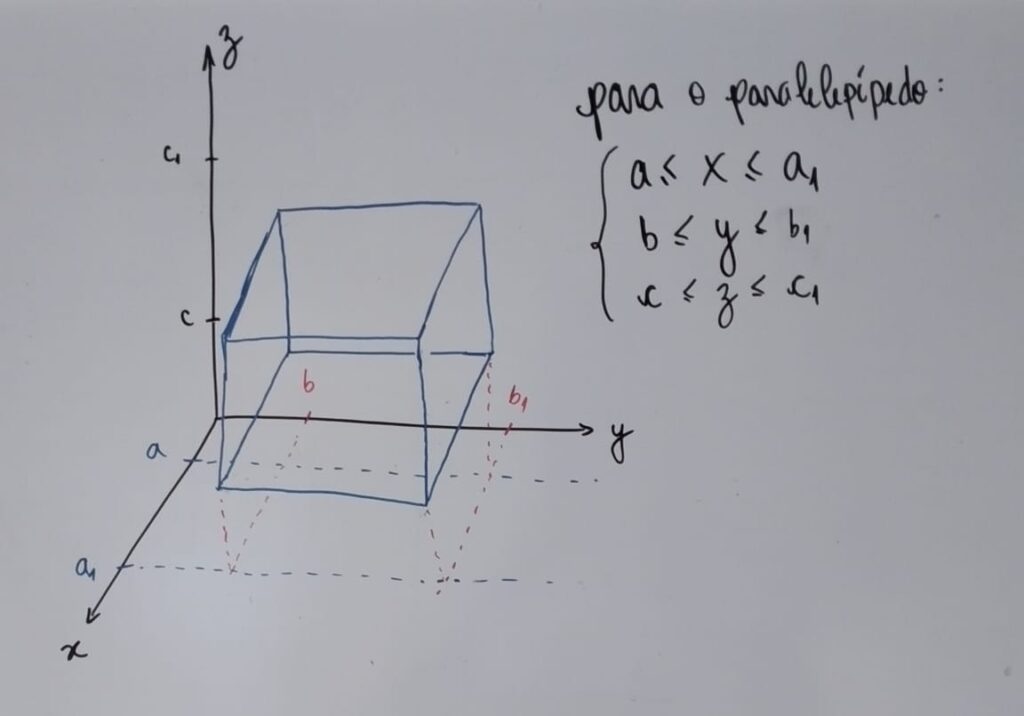
P2 { b=yo< y1 < y2 < ... < yn = b1 }
P3 { c=zo< z1 < z2 < ... < zn = c1 }
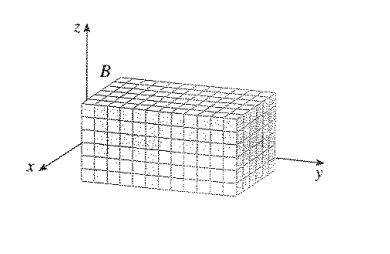
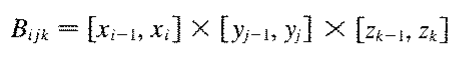
É razoável pensarmos então que a caixa por completo é a soma de todas subcaixas de Oxyz. E ainda elas podem ser moldadas por um função f(x,y,z). Podemos então colocar essa expressão na soma de Riemann:
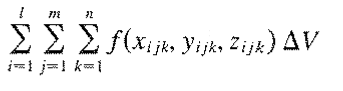
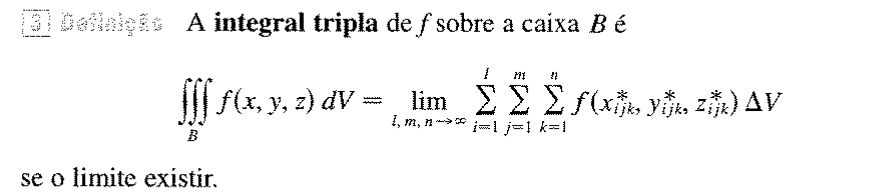


Exemplo Resolvido:
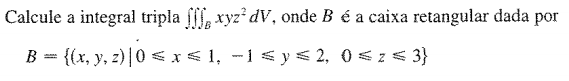

2. Definição de Integral Tripla como um domínio Genérico.
No exemplo anterior vimos que a integral tripla calculada é uma integral no qual x, y e z são definidos por valores constantes e não por funções. Mas a partir desse exemplo podemos definir uma integral em que um domínio é descrito por uma função.
Vamos partir do pressuposto de que há uma região genérica E no qual está contida em um paralelepípedo.
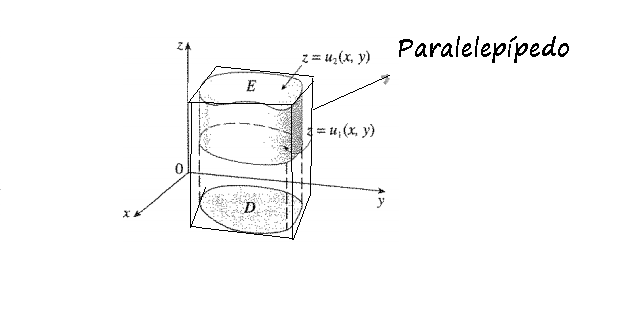
Vamos definir uma função F(x,y,z) no qual os valores de dentro de E contribuam a valores de uma somatória e os valores de fora de E, não contribuam para os mesmos. (Obs o quadro consta F(x,y) mas na verdade são F(x,y,z).

Se essa função F(x,y,z) for definida podemos dizer então que:
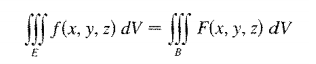
O autor do livro James Stwert Vol II, baseia esses domínios genéricos como 3 tipos:
- 1°tipo: O domínio é baseado em funções que dependem de x e y – u(x,y).



De forma muito parecida são definidas a região E do tipo 2 e 3. DICA: Não fique preso a tipos e fórmulas, tudo vem da interpretação tenha consciência do que está manipulando.


Volume de E = ∫∫∫Edv
Volume de E = ∫∫∫Edxdydz
Realmente é muita informação para lidar de uma vez, mas depois de alguns exercícios você vai ver que esses pensamentos ficam mais naturais do que técnicos, pois no final, tudo deve respeitar as leis matemáticas e as definições básicas das integrais. Vamos resolver uns exercícios para tudo ficar mais claro!
Exercícios Resolvidos:



Respostas: