O efeito da refração quando a onda eletromagnetica atravessa uma superficie que divide dois meios. Cada meio possui suas próprias características eletromagnéticas, causando uma variação na direção de propagação de uma onda devido a mudança de velocidade da onda.
A lei da refração foi formulada pelo matemático e astrônomo holandês Willebroad Snellius (Conhecido então como Snell), e também formulada por Descartes no qual essa lei conseguiria mensurar a relação entre os ângulos de incidência e de refração com uma característica do meio chamada de índice de refração, no qual estudaremos nessa aula.
Acesse as aulas anteriores:
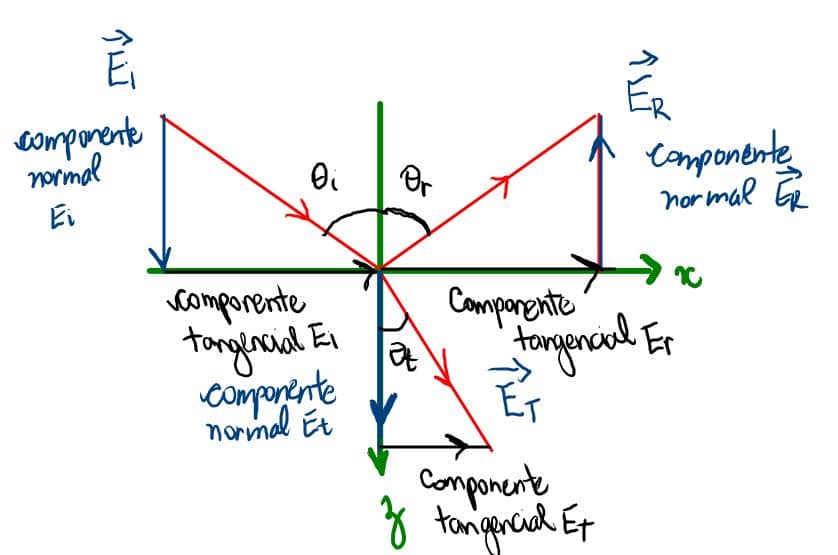
Assim como visto na aula anterior (leis da reflexão), definimos essas leis a partir da seguinte igualdade:
\large{\vec{\gamma}_i.\vec{r}_s = \vec{\gamma}_r.\vec{r}_s = \vec{\gamma}_t.\vec{r}_s}
Iremos buscar entender a lei da refração a partir da igualdade:
(1) \large{\vec{\gamma}_i.\vec{r}_s = \vec{\gamma}_t.\vec{r}_s}
Já que foram definidos os vetores de propagação em leis da reflexão \vec{\gamma}_i e \vec{\gamma}_r e \vec{\gamma}_t, e o plano de localização de pontos \vec{r}_s
Sabendo que \vec{\gamma} = \hat{\gamma}. \gamma, podemos substituir tais definições na equação (1), assim teremos:
\large{\hat{\gamma}_i. \gamma_i . \vec{r}_s = \hat{\gamma}_t. \gamma_t . \vec{r}_s }
(2) \large{\gamma_i. \hat{\gamma}_i.(x\hat{x} + y\hat{y}) = \gamma_t. \hat{\gamma}_t.(x\hat{x} + y\hat{y})}
Considerando a aula anterior as seguintes definições:
(i) \large{\hat{\gamma}_i = \frac{\vec{\gamma}_i }{\gamma_i} = sen(\phi_i) \hat{x} + cos(\phi_i) \hat{z}}(ii) \large{\hat{\gamma}_t = \frac{\vec{\gamma}_t }{\gamma_t} = sen(\phi_t) \hat{x} + cos(\phi_t) \hat{z}}Unindo as equações (2) com (i) e (ii):
\large{\gamma_i.(sen(\phi_i) \hat{x} + cos(\phi_i) \hat{z}).(x\hat{x} + y\hat{y}) = \gamma_t . (sen(\phi_t) \hat{x} + cos(\phi_t) \hat{z}).(x\hat{x} + y\hat{y})}Fazendo o produto escalar, temos que:
\large{\gamma_i. sen(\phi_i) x = \gamma_t . sen(\phi_t) x}\large{\gamma_i. sen(\phi_i)\cancel{ x } = \gamma_t . sen(\phi_t) \cancel{ x }}\therefore \boxed{\Large{\frac{sen\phi_i}{sen\phi_t} = \frac{\gamma_t}{\gamma_i} = \sqrt{\frac{\mu_2.(\sigma_2 + i\omega\epsilon_2)}{\mu_1 .(\sigma_1 + i\omega\epsilon_1)}}}} \to Lei Descartes-Snell