Quando uma onda eletromagnética se propaga de um meio para outro, ocorrem muitos fenômenos importantes. Cada meio é caracterizado pela sua formação atômica e suas interações elétricas com uma onda eletromagnética podem afetar a velocidade das ondas, assim como podem apresentar dificuldades na propagação dos mesmos.
Haja vista que cada meio possui seu próprio coeficiente de atenuação, de fase que dependem de propriedades como a permissividade elétrica, a condutividade elétrica e a permeabilidade elétrica, que se relacionam com a frequência que essa onda é propagada.
Vejamos que toda teoria tem uma base sólida dos fundamentos elementares da ciência. E a partir do chama condições de contorno, podemos desenvolver as leis da reflexão e da refração (ou transferência) da onda de um meio à outro.
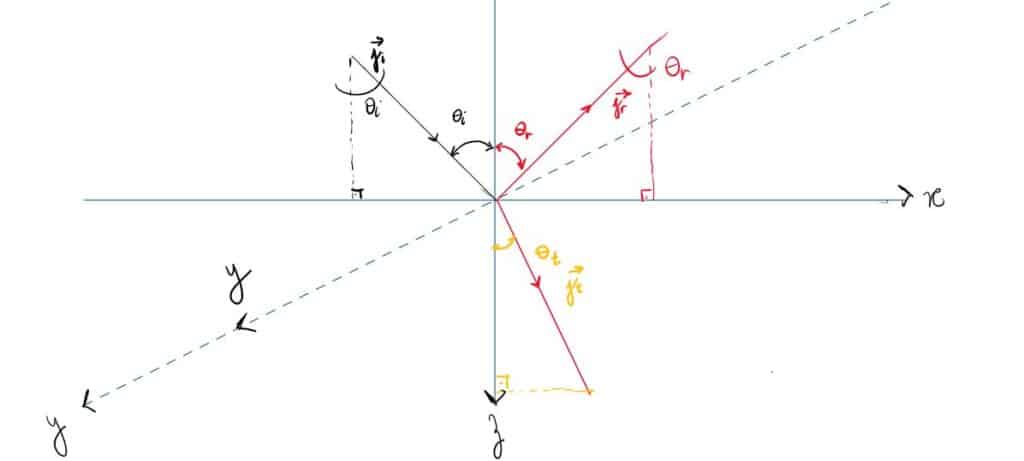
Para definirmos tais leis, devemos satisfazer as condições da superfície de contorno na superfície de separação entre os meios.
Condição de continuidade da componente tangencial do campo elétrico:
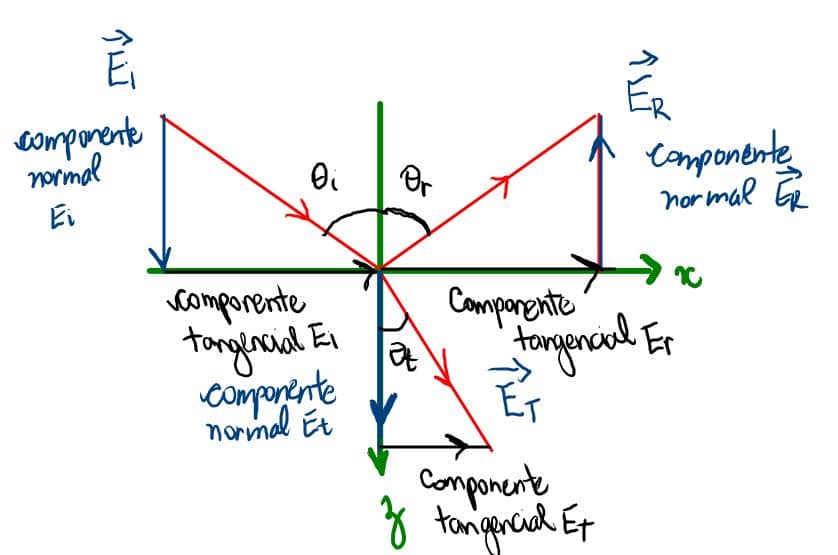
Vejamos que tanto a onda E_i, E_r, E_t possuem uma componente tangencial e uma componente normal a superfície. Vejamos que assumimos que z = 0 será nossa superfície.
Sobre a superfície S, temos portanto a seguinte condição:
\hat{n} \times \vec{E}_1 = \hat{n} \times \vec{E}_2
A normal de acordo com a figura acima é dada no eixo z. Na interface do meio 1, temos uma sobreposição de ondas, ou seja, a existência da onda incidente e da onda refletida. Portanto o lado exquerdo da condição fica:
\large{z \times \left(\vec{E}_{io}.e^{-\vec{\gamma_i}.\vec{r}_s} + \vec{E}_{ro} . e^{-\vec{\gamma_r}.\vec{r}_s}\right) = z \times \vec{E}_{to}.e^{-\vec{\gamma_t}.\vec{r}_s}}
Visto que na aula anterior foi definido os componentes E_i, E_r, E_t e H_i, H_r, H_t, assim como seus respectivos vetores de progagação.
A condição de continuidade deve não depender do vetor posição que se encontra no plano divisório \vec{r_s} , assim as exponenciais da equação acima devem ser iguais, de modo que portanto, as suas potências devem ser iguais. Portanto:
\large{\vec{\gamma_i}.\vec{r}_s = \vec{\gamma_r}.\vec{r}_s = \vec{\gamma_t}.\vec{r}_s }
Da igualdade acima podemos concluir que:
\large{\vec{r_s}.\left(\vec{\gamma}_i – \vec{\gamma}_r \right) = 0 }
Tirando a conclusão que a partir do produto escalar da formula acima, temos que o vetor \vec{r_s} é perpendicular ao plano que os vetores de propagação estão, de forma que os vetores de propagação formam um plano chamado plano de incidência.
1ª lei da reflexão: vetores de propagação da onda incidente e onda refletida são clopanares, no qual o plano a que pertencem é perpendicular à interface entre dois meios. A onda incidente e refletida pertencem ao plano de incidência e este mesmo plano é perpendicular ao plano de reflexão.
Vejamos na figura abaixo:
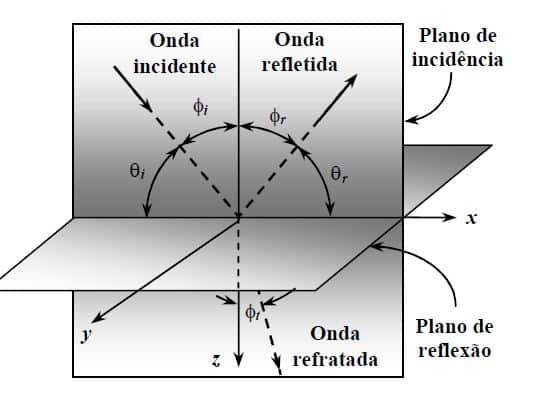
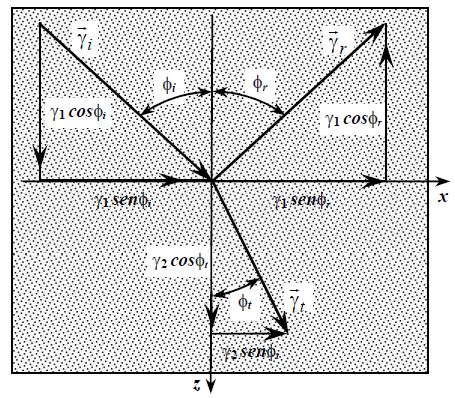
Fazendo a análise geométrica a partir dos conceitos de trigonometria, temos que:
(1) \vec{\gamma}_i = \gamma_i . sen(\phi_i) \hat{x} + \gamma_i . cos(\phi_i) \hat{z}(2) \vec{\gamma}_r = \gamma_r . sen(\phi_r) \hat{x} – \gamma_r . cos(\phi_r) \hat{z}(3) \vec{\gamma}_t = \gamma_t . sen(\phi_t) \hat{x} + \gamma_t . cos(\phi_t) \hat{z}Pelos conceitos de Geometria Analítica temos que um vetor unitário (aquele que expressa a unidade básica de um vetor, é dado por:
(4) \large{\hat{\gamma} = \frac{\vec{\gamma}}{|\vec{\gamma}|}}
Utilizando as fórmulas (1), (2) e (3) aplicado a fórmula (4), temos que, ou seja, expressando as fórmulas (1), (2) e (3) em termos de seus vetores unitários temos que:
(5) \large{\hat{\gamma}_i = \frac{\vec{\gamma}_i }{\gamma_i} = sen(\phi_i) \hat{x} + cos(\phi_i) \hat{z}}(6) \large{\hat{\gamma}_r = \frac{\vec{\gamma}_r }{\gamma_r} = sen(\phi_r) \hat{x} – cos(\phi_r) \hat{z}}(7) \large{\hat{\gamma}_t = \frac{\vec{\gamma}_t }{\gamma_t} = sen(\phi_t) \hat{x} + cos(\phi_t) \hat{z}}Voltando a fórmula dada por: \large{\vec{\gamma_i}.\vec{r}_s = \vec{\gamma_r}.\vec{r}_s = \vec{\gamma_t}.\vec{r}_s } -> (definido anteriormente)
Podemos juntar o negócio todo. Ou seja:
\large{\vec{\gamma_i}.\vec{r}_s = \vec{\gamma_r}.\vec{r}_s}Portanto, temos a igualdade:
\large{(sen(\phi_i) \hat{x} + cos(\phi_i) \hat{z}). \vec{r}_s = (sen(\phi_r) \hat{x} – cos(\phi_r) \hat{z}}). \vec{r}_sGerando o seguinte produto escalar:
\large{(sen(\phi_i) \hat{x} + cos(\phi_i) \hat{z}). (x\hat{x} + y\hat{y}) = (sen(\phi_r) \hat{x} – cos(\phi_r) \hat{z}}). (x\hat{x} + y\hat{y})Desenvolvendo o produto escalar, temos o seguinte resultado:
\large{x.sen(\phi_i) = x.sen(\phi_r)}Concluimos a segunda lei da reflexão! Onde:
\large{\phi_i = \phi_r}
Segunda lei da Reflexão: O ângulo de incidência e o ângulo de reflexão são iguais, independente dos meios de propagação sobre qualquer comprimento de onda.