Limite de uma função:

Em termos simples, o limite de uma função em um ponto se refere ao valor que a função se aproxima à medida que a entrada (ou variável independente) se aproxima de um certo valor. Este conceito é crucial para entender como as funções se comportam perto de pontos específicos e é a base para definições mais complexas como a derivada e a integral.

Limite de uma função Quadrática: Um Exemplo Prático

Para darmos introdução aos limites de uma função, vamos analisar o comportamento de uma função qualquer. Nosso exemplo usaremos a função $f(x) = x^2 - x + 2.$

Analisando os valores de y = f(x) para valores de x que se aproximam de 2, temos a seguinte tabela:

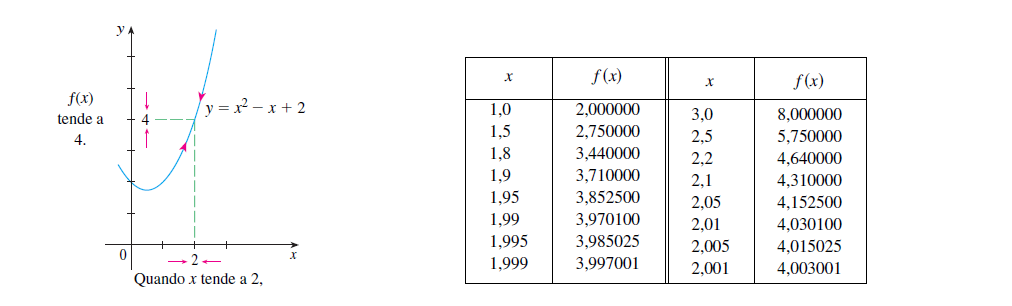
Veremos mais a frente sobre limites laterais, onde os valores se aproximam tanto da esquerda como da direita.

Observação: A medida que os valores de x vão se aproximando de 2, os valores de f(x) vão se aproximando de 4. Apenas olhe a tabela. Então podemos expressar da seguinte maneira:

“O limite de f(x) quando x tende a 2 é igual a 4.”

Ou seja, descrevemos matematicamente da seguinte maneira:

$\lim_{x \to a} f(x) = L$

Definição do Limite de uma Função:

Supondo que o domínio de f(x) esteja definido em algum intervalo aberto que contenha a, exceto o próprio a, então temos que:

$\lim_{x \to a} f(x) = L$
“O Limite de f(x), quando x tende a “a”, é igual a L.

Se pudermos tornar os valores de f(x) suficientemente e arbitrariamente próximos do valor L, tornamos os valores de x suficientemente próximos de a, porém não igual a “a”.

De grosso modo:

Os valores de f(x) tendem a ficar mais próximos de L, a medida que x tende a ficar mais próximos de a, mas x é diferente de a.

Observe que f(x) só precisa estar definido em valores próximas de a, porém não sequer precisa estar definido em x=a. Olhe a próxima figura e observe a diferença entre esses 3 gráficos:

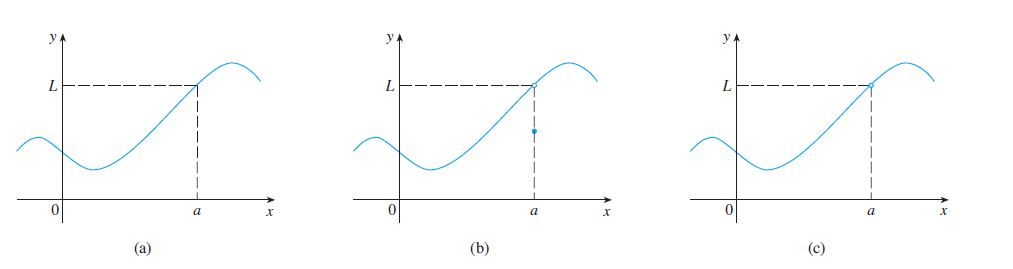
Vamos aprender inúmeras formas de calcular limites. Iremos ver que podemos calcular de forma algebrica, de forma gráfica, utilizando métodos como de l’Hospital, assim como estimativas. Nesse primeiro momento vamos calcular utilizando estimativas matemáticas.

Exemplos resolvidos:

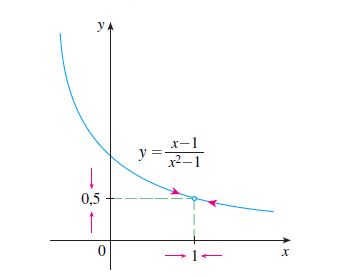
Exemplo 1: Calcule o $lim_{x \to 1}{\frac{x-1}{x^2-1}}$ a partir de estimativas.

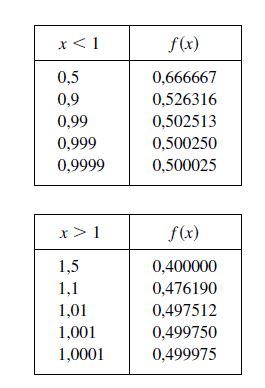
Resposta: Inicialmente o nosso objetivo é calcularmos diversos valores de f(x), onde x vai se aproximando de x = 1 tanto pela esquerda como para direita. Vamos pegar a fórmula do limite e simplesmente substituir por valores cada vez mais próximos de x = 1.

Assim calculamos de valores de x<1 até x=1 e de x>1 até x =1;

Para   x = 0,5;   Temos  f(0,5) = \lim_{x \to 1}{\frac{0,5 – 1}{(0,5)^2 – 1}} = 0,6666667

Para   x = 0,9;   Temos  f(0,9) = \lim_{x \to 1}{\frac{0,9 – 1}{(0,9)^2 – 1}} = 0,526316

Para   x =   0,99;   Temos  f(0,99) = \lim_{x \to 1}{\frac{0,99 – 1}{(0,99)^2 – 1}} = 0,502513

Para   x =   0,999;   Temos  f(0,999) = \lim_{x \to 1}{\frac{0,999 – 1}{(0,999)^2 – 1}} = 0,500250

Para   x =   0,9999;   Temos  f(0,9999) = \lim_{x \to 1}{\frac{0,9999 – 1}{(0,9999)^2 – 1}} = 0,500025

Veja que nos estamos aproximando de x = 1 por valores menores do que 1. E assim chegamos cada vez mais próximos de f(0,999…) = 0,5000…

Portanto:

$\boxed{lim_{x \to 1^-}{\frac{x-1}{x^2-1}} =0,5}$

Vindo de valores mais altos que x = 1, ou seja para x tendendo para 1 pela direita temos:

Para   x =   1,5;   Temos   f(1,5) = \lim_{x \to 1}{\frac{1,5- 1}{(1,5)^2 – 1}} = 0,4000000

Para   x =  1,1;   Temos   f(1,1) = \lim_{x \to 1}{\frac{1,1- 1}{(1,1)^2 – 1}} = 0,476190

Para   x =   1,01;   Temos   f(1,01) = \lim_{x \to 1}{\frac{1,01- 1}{(1,01)^2 – 1}} = 0,497512

Para   x =   1,001;   Temos   f(1,001) = \lim_{x \to 1}{\frac{1,001- 1}{(1,001)^2 – 1}} = 0,499750

Para   x =   1,0001;   Temos   f(1,0001) = \lim_{x \to 1}{\frac{1,0001- 1}{(1,0001)^2 – 1}} = 0,499975

Portanto:

$\boxed{lim_{x \to 1^+}{\frac{x-1}{x^2-1}} =0,5}$

Assim concluímos que:

$\boxed{lim_{x \to 1}{\frac{x-1}{x^2-1}} = 0,5}$

Exemplo 2: Calcule o $lim_{t \to 0}({\sqrt{ (t^2 + 9) } – 3})/t^2$ a partir de estimativas.

Vejamos que utilizamos do mesmo passo a passo para calcular tal limite por estimativa. Ou seja vamos supor diversos valores maiores e menores que t = 0 de modo a chegarmos na conclusão dos valores mais próximos de um limite descrito em exercício.

Assim utilizamos o mesmo método, chegamos nos seguintes valores:

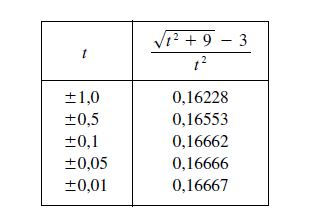
Chegamos a conclusão de que:

\boxed{lim_{t \to 0}{(\sqrt{t^2+9}   –  3)}/t^2  = \frac{1}{6}}