1. Equações de Fresnel

Vimos anteriormente que quando uma onda eletromagnética atinge uma superfícies que separam dois meios, acontece o fenômeno de reflexão e refração. Ou seja uma energia inicial da onda incidente $\vec{E}_i$ depois que atravessar a superfície haverá duas energias, no qual representarão a onda refletida e a onda refratada, respectivamente $\vec{E}_r$ e $\vec{E}_t$ .

As equações de Fresnel irão analisar e relacionar a onda incidente com a onda refletida e a onda transmitida em forma de duas equações, no qual são diretamente proporcionais com o coeficiente de reflexão e coeficiente de transmissão (ou refração).

Em outras palavras com o uso das equações de Fresnel junto com algumas condições que iremos especificar posteriormente seremos capazes de calcular a equação da onda refletida e transmitida a partir da equação da onda incidente.

Conteúdos Anteriores:

2. Decomposição da Onda Incidente:

Observe a figura abaixo:

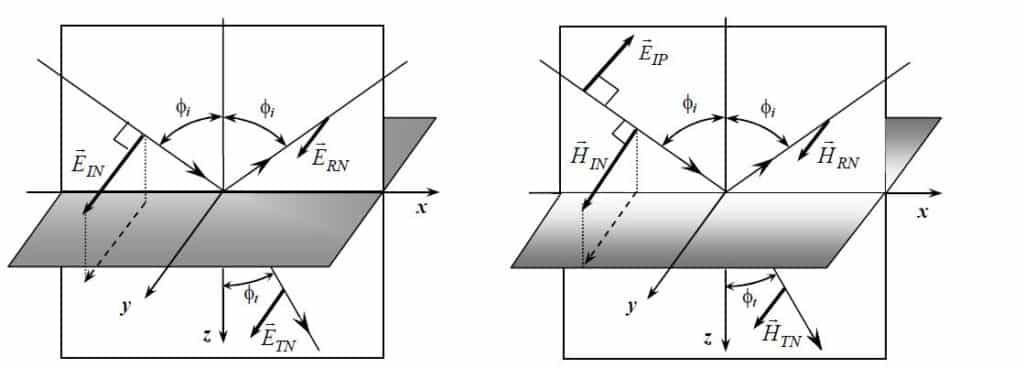
A quantização da onda incidente, seja ela magnética ou elétrica é necessário conhecer a polarização que essa mesma possui e o ângulo desse vetor em relação à normal da superfície que separam os dois meios.

(a) Onda transversal Elétrica (TE) ou onda com Polarização normal. Significa que a onda elétrica tem sua direção de propagação normal ao plano de incidência (O plano branco na figura). Visto na figura da esquerda.

(b) Onda transversal Magnética (TM) ou onda com Polarização paralela. Significa que a onda magnética tem sua propagação normal ao plano de incidência. (O plano branco na figura).

3. Relação entre Ondas no Fenômeno de Reflexão e Refração:

Coeficiente de Reflexão( $\Gamma$ ): É um coeficiente que relaciona a amplitude da onda incidente com a amplitude da onda refletida.

Coeficiente de Refração( $\Tau$ ): É um coeficiente que relaciona a amplitude da onda Incidente com a amplitude da onda refratada ou transferida.

O cálculo de cada um dos coeficientes referidos acima dependem se a onda é Transversal Elétrica (TE) ou se a onda é Transversal Magnética (TM).

(A) Para o caso da onda elétrica com Polarização Normal ao plano de Incidência: Com referência ao espaço esquerdo da figura acima, temos os componentes elétricos atingindo o plano de reflexão, no qual é válida as seguintes expressões:

Relação amplitude da onda incidente com a onda refletida $(1) \boxed{\vec{E}_{RN} = \Gamma_{EN} * \vec{E}_{IN}}$

Relação amplitude da onda incidente com a onda transferida $(2) \boxed{\vec{E}_{TN} = \Tau_{EN} * \vec{E}_{IN}}$

Vejamos então que no caso (a) o campo elétrico é normal ao plano de incidência e o campo magnético é paralelo ao mesmo.

(b) Para o caso da onda elétrica com Polarização paralela ao plano de incidência: Seria mais conveniente trabalhar com as componentes magnéticas normais ao plano de incidência. De modo que:

Relação amplitude da onda incidente com a onda refletida $(3) \boxed{\vec{H}_{RN} = \Gamma_{HN} * \vec{H}_{IN}}$

Relação amplitude da onda incidente com a onda transferida $(4) \boxed{\vec{H}_{TN} = \Tau_{HN} * \vec{H}_{IN}}$

Seguindo as condições de contorno, temos que:

\vec{E}_{IN} + \vec{E}_{RN} = \vec{E}_{TN}

As equações de Fresnel começam a serem desevolvidas pelas condições de contorno acima, no qual: