Relembrando a última aula da relação entre funções e conjuntos, temos essa figura:
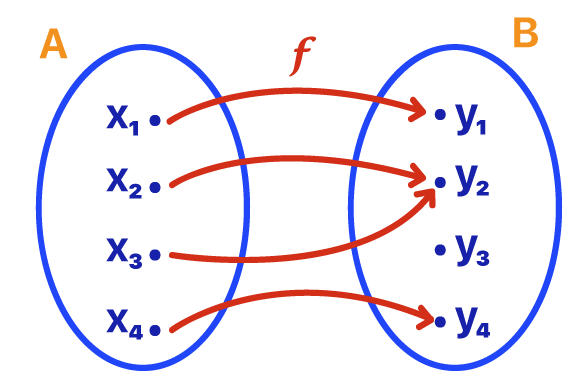
Resumindo o que está acontecendo é o seguinte: Valores que são pertencentes ao conjunto A estão sendo transformados por uma função f para valores do conjunto B. Dizemos então que f:A -> B , certo? Nesse caso da figura temos: f(x1) = y1, f(x2) = y2 , f(x3) = y2 e f(x4)=y4.
1) Domínio de uma função:
Domínio de uma função: É o conjunto máximo de valores em que a função está definida. Em outras palavras, são o conjunto de valores de x, no qual existirá valores de f(x) ou y. Dizemos também que são os valores de entrada, são os valores em que ainda estão para ser transformados pela função f e eles matematicamente podem ser transformados pela função f.
Mas o que não pode ser transformado por uma função? Um exemplo é um número dividido por zero. Um valor dividido por zero não existe, não está definido para o valor de uma função. Ou seja f(x) = 1/x, o valor x =0 não deve ser do domínio de f, uma vez que f(0) = 1/0 = NÃO EXISTE.
No caso dos conjuntos: São os valores que pertencem ao conjunto A da figura, portanto A = { x1, x2,x3,x4 } porque são os valores de entrada, são aqueles de f(x) realmente existe e são os valores que estão no conjunto B. Portando definimos da seguinte forma: Dom f ={x1, x2,x3,x4 } .
2) Contra-Domínio de uma função:
São todos os valores possíveis de f(x) ou y. No caso dos conjuntos, dizemos que o contra-domínio são os valores de y em que pertencem ao conjunto B. (Eles são considerados o contra-domínio mesmo que não esteja correspondendo a nenhum valor de x – ou seja, não importa se não há nada apontando para esse valor de y – ). Observe o valor y3 que mesmo não sendo apontado por nada, participa do CD.
O contra domínio de f no caso da figura a cima é: CD f = {y1, y2 , y3 , y4}.
3) Imagem de uma função:
É o conjunto de valores gerados pelo domínio dessa mesma função. Então se valores de x são transformados por uma função f, gerando valores de Y, esses valores de y são a Imagem dessa mesma função.
De uma forma mais técnica, dizemos: f:X -> Y e Y é o conjunto imagem de f. Também é correto dizer: f(x) = y, tal que os valores de x são o domínio e os valores de y (ou f(x)) são a imagem de f.
No caso dos conjuntos: São os valores de y que correspondem aos valores de x. Ou seja, são valores que pertencem ao conjunto B, e também devem estar relacionados aos valores de x (do conjunto A). Na prática são os valores de y que participam do conjunto B e estão sendo “apontados” por valores de x do conjunto A.
Dizemos da figura acima que Im(f) = { y1, y2 , y4}.
Exemplo resolvido:






