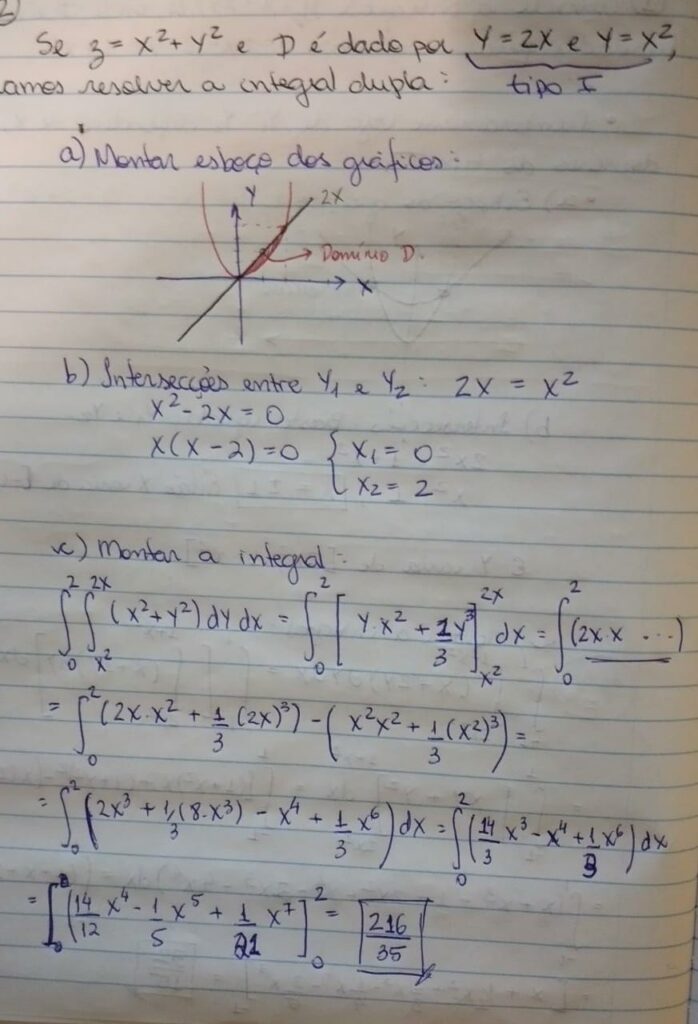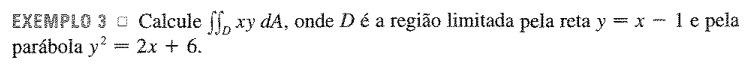1. Introdução:
Na aula passada aprendemos como calcular integrais duplas sobre regiões retangulares. Resumidamente dividimos os retângulos em vários sub-retângulos de forma que suas sub-áreas multiplicadas por f(x,y) nos daria o volume dessa subdivisão e a somatória desses volumes nos dariam um valor muito preciso da área do sólido sobre o retângulo e abaixo de z = f(x,y).
Porém a pergunta é: Como podemos calcular o volume de um sólido sobre uma região qualquer? Podemos estender os conceitos do domínio retangular, e colocar qualquer um domínio qualquer dentro dessa região retangular, de forma que a partir de uma condição de soma, poderíamos determinar sub-áreas de domínio qualquer e depois multiplica-los por f(x,y) afim de chegar em uma somatória de mini-volumes para chegar ao volume que queremos. Vamos dar uma olhada mais profundo nesse conceito.
2. Definindo f(x,y) em um domínio genérico D:
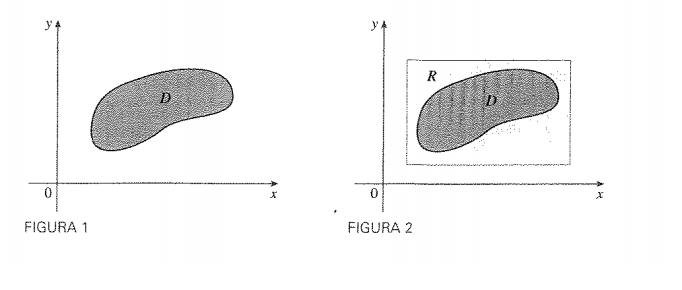
- Primeiramente vamos considerar um domínio D genérico no qual ele é limitado. Lembre-se que qualquer domínio limitado pode ser colocado dentro de um retângulo R;
- Em segundo lugar ainda pensando nos domínios retangulares podemos sair do pressuposto de que todo domínio de B pertence a R porém nem todo os valores de R pertencem ao domínio de D;
- Para o conjunto de valores de R que não pertencem a D devemos considerar valores de f(x,y) = 0 – Uma vez que f(x,y) está sobre uma região genérica e não retangular. Logo definimos:
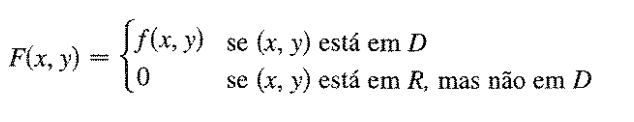
Portanto caso F(x,y) definido dessa forma e a integral dupla sobre o retângulo existir, definimos a integral dupla de f sobre D:

Observe que se os valores (x,y) de f(x,y) pertencer a R e a D, temos uma contribuição no valor do volume do sólido, porém caso (x,y) pertencer apenas em R e não a D, não contribuição alguma no volume. A partir desse ideal a formula 1 se torna razoável. Não importa qual maior o domínio R seja tomado, a única importância é D ∈ R.
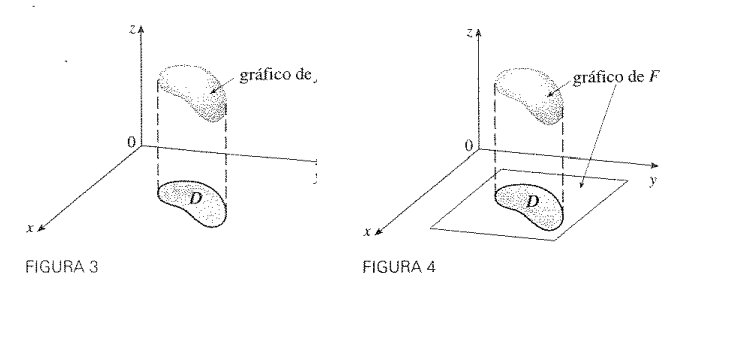
3. Volume do Sólido Acima da Região Genérica D:
V = ∫∫Df(x,y)dA.
O livro do James Stwert Vol II, classifica a região D em dois tipos;
a) Tipo I : Essa região é formada por dois gráficos de funções de x. Definimos o domínio da seguinte forma:
E alguns gráficos do domínio D do tipo 1 podem ser representados da seguinte forma:
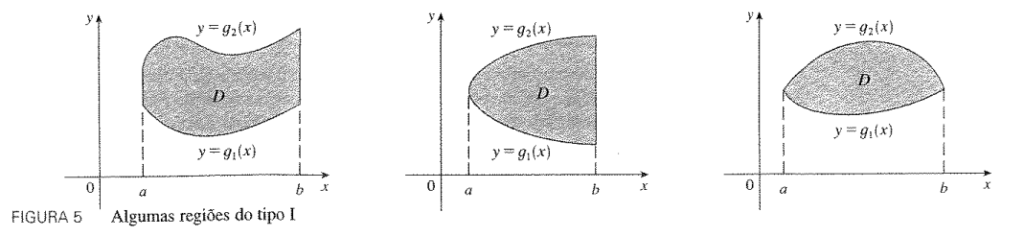
A integral pode ser expressa então:

Podemos expressar a integral dupla da seguinte maneira:

b) Tipo II : Essa região é formada por dois gráficos de funções de y. Definimos o domínio da seguinte forma:
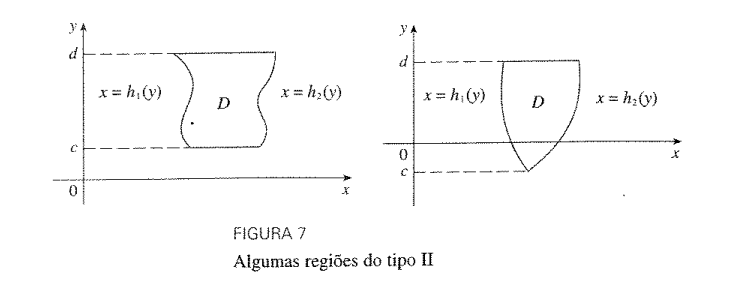

4. Método para Resolver Exercícios de Integrais Duplas em Regiões Genéricas:
Eu como estudante, ao fazer muitos exercícios, pensei em um método ótimo para resolver esses tipos de integrais duplas:
- Esboçar os gráficos que formam o domínio D, ou seja, desenhar B no plano Oxy.
- Descobrir os pontos onde o domínio começa e onde termina. (Geralmente é a intersecção entre os gráficos.)
- Montar a integral dupla de forma a organizar os limites integrantes (Sempre de baixo -> cima ou esquerda -> direita.)
- Resolver a integral dupla.
Claro que só descrevendo dessa forma fica complicado, mas vendo os exercícios resolvidos ficará mais claro.
Lembre-se de beber água!
Exemplos resolvidos: