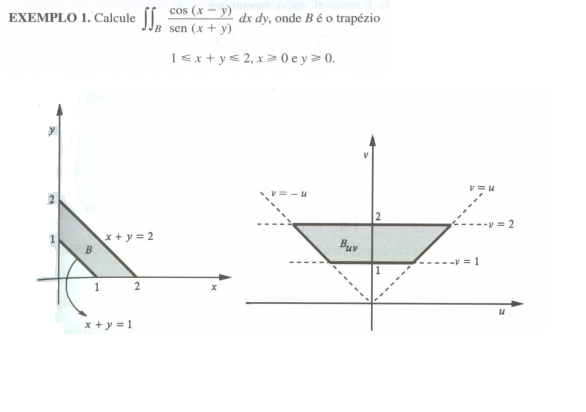
1.Introdução
A mudança de variáveis em uma integral é muito importante para situações no qual o domínio da função ou f(x,y) ficam muito difícil de resolver apenas usando as matérias anteriores. O fato é de que mudando as variáveis faz com que o domínio D e f(x,y) sejam manipuladas mais facilmente, assim como a própria integral fica mais fácil de ser resolvida.
2. Definindo a mudança de variáveis:
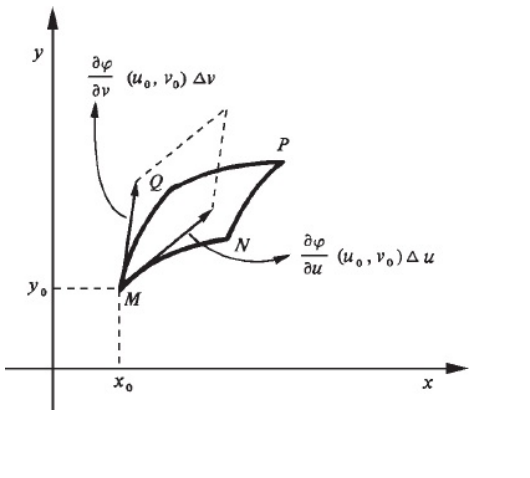
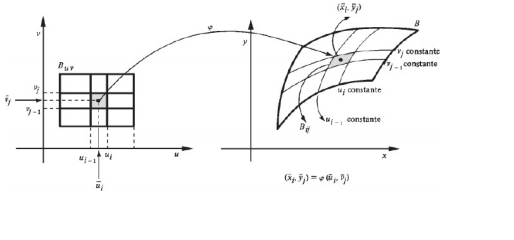
Se temos um domínio retangular, no qual A {(u,v)| uo ≤ u ≤ uo + Δu, vo ≤ v ≤ vo+Δv} temos a figura dada abaixo:
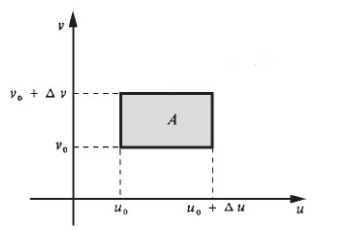
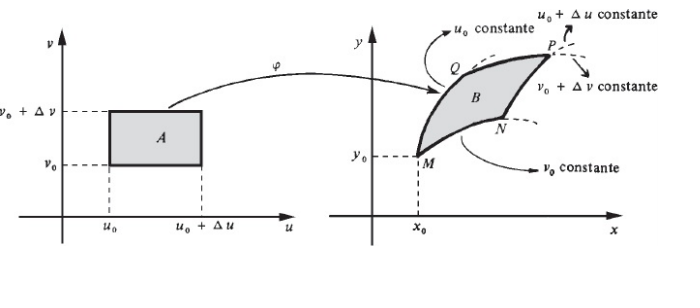
Como a integral dupla surgiu primordialmente para resolver problemas de volumes de sólidos (Aula 1 – https://breakthescience.com.br/integrais-multiplas/ ) Devemos partir daí para entendermos a mudança de variáveis.
Logo se V = Ab .h , vamos explorar a área da base de B cujo provém de φ(A).
Primeiramente vamos identificar como se calcula o comprimento S de um arco de uma curva dada por e γ (t) = (x(t), y(t)), além disso consideremos dois pontos γ (t) e γ (a), no qual a é um ponto fixo.
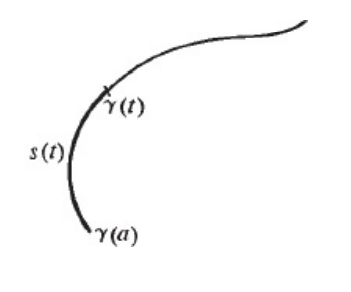
Visto as matérias Calculo I e II, entendemos que podemos determinar o comprimento s(t) a essa curva, a partir da somatória dos valores tangentes da curva que vão de ponto a ponto de (a -> t). Logo podemos expressar usando a integral: (Lembre-se que a tangente de f(x) em x é a derivada da mesma, logo tanγ = y’).
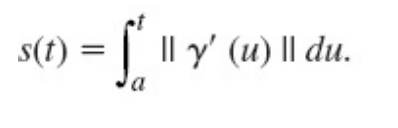
Podemos transformar tal integral em uma equação diferencial: ds = || γ’ (t) || dt
De modo que o valor da variação de s(t) pode ser dado como:
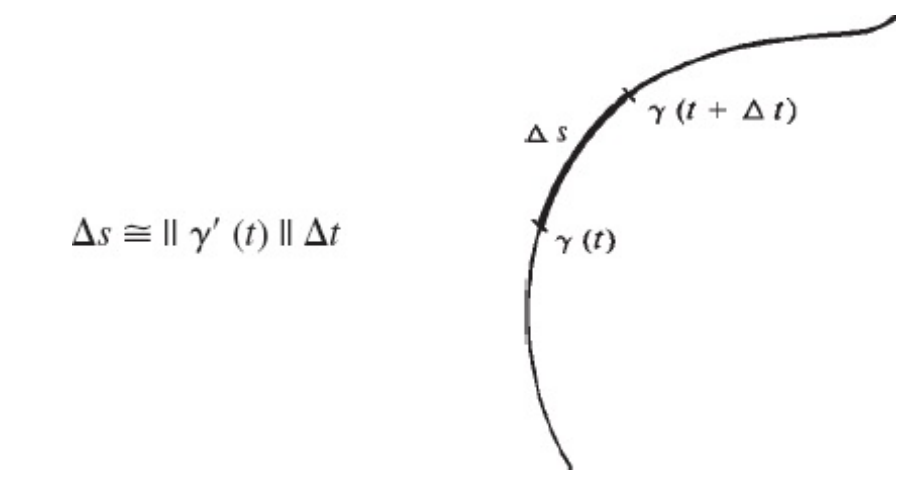
onde Δs é o comprimento do arco de extremidades γ (t) e γ (t + Δt), com Δt > 0. Evidentemente, a aproximação será tanto melhor quanto menor for Δt.
Voltando a situação anterior no qual o domínio B é expresso graficamente na figura 2 (A figura da direita) podemos introduzir dois vetores tangentes à curva u e à curva v.

desempenha (em relação à curva v ∞ φ (u, v)) o mesmo papel que γ’ (t). Pelo que vimos acima.
A seguinte pergunta é: Mas para que tudo isso? O que faremos com esses dois vetores introduzidos? E aí que a coisa fica interessante! Pois na Geometria Analítica aprendemos que o módulo do produto vetorial de dois vetores n são interpretados como a área do plano gerado pelos vetores. Logo usaremos isso como álgebra para determinar a área do domínio B.
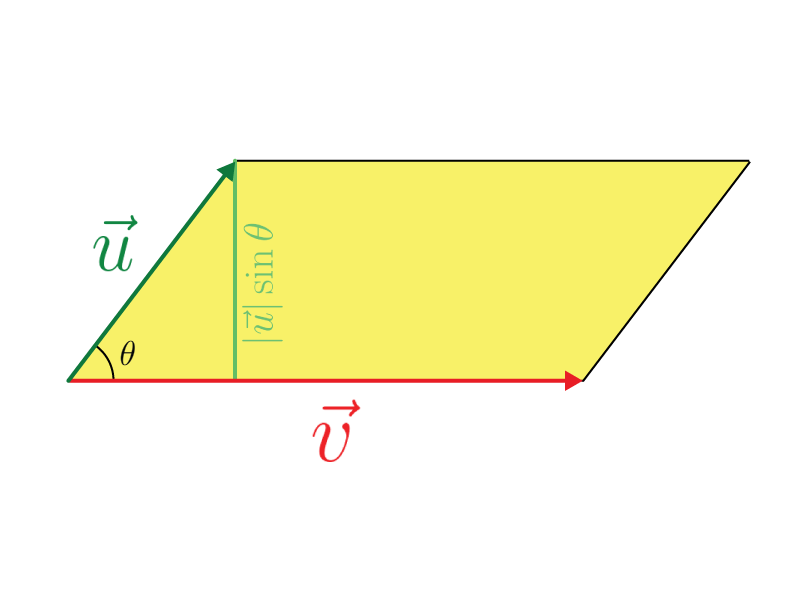

Podemos definir a área de B como:

Para calcularmos o produto vetorial de dois vetores a Álgebra Linear e Geometria Analítica nos deixa o presente das matrizes no qual é dada pela seguinte formula:

3.Integrais duplas e mudança de variáveis:
Depois que entendido o tópico de cima, tudo fica mais simples. Pois uma integral não é nada mais que a somatória de minúsculos volumes de um sólido chegando ao valor do volume real desse sólido. Então fazemos sub-divisões no domínio de A e consequentemente a transformação para B também terá essas partições.
Essas divisões que geram mxn retângulos menores pode ser calculado a partir do módulo do produto vetorial descrito em cima.

4. Exercícios Resolvidos