Nas aulas passadas foram estudados como as ondas eletromagnéticas se comportam em um meio ilimitado. Vimos a interdependencia entre os campos elétricos e magnéticos, no qual ambos sempre existem de forma mútua. Mas agora a grande pergunta é: E se uma onda elétromagnética ir de um meio para o outro, o que aconteceria?
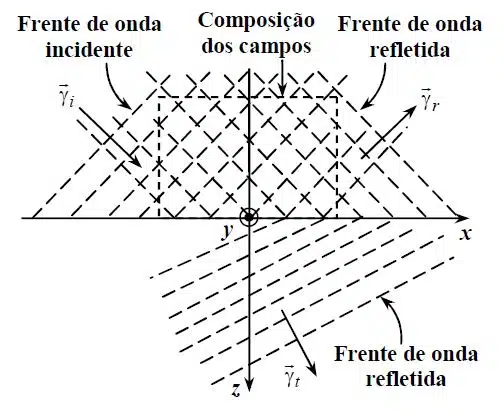
Quando uma onda eletromagnética passa de um meio para outro, uma parte da onda é transferida ou refratada, e parte a outra parte da onda é refletida. Portando ocorre um fenômeno de reflexão e refração da onda.
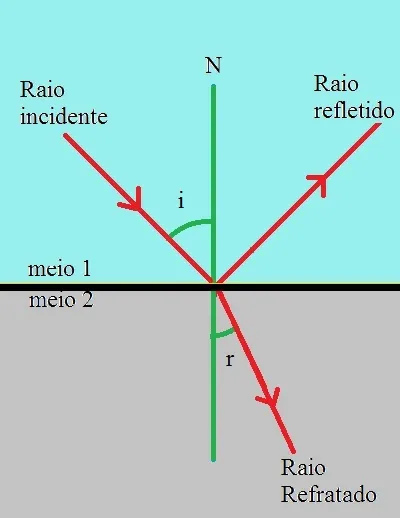
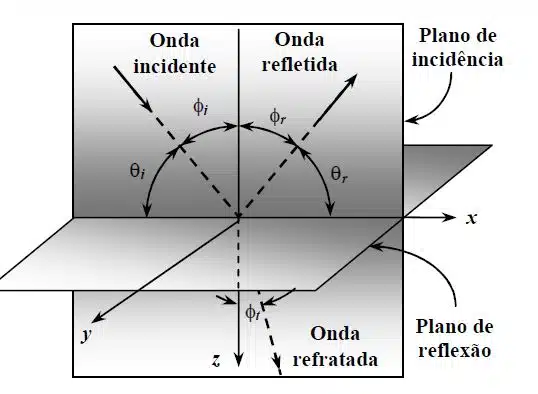
O que significa parte da onda ser refletida e parte da onda ser refratada? Significa que parte da energia da onda incidente “fica” no meio 1 e parte da energia da onda incidente “passa” para o meio 2.
Assim, em consequencia desse fenômeno, agora, o que era a onda incidente anteriormente, torna-se a formação de duas ondas eletromagnéticas: Onda eletromagnética refletida e onda eletromagnética refratada.
E vejamos que essas ondas eletromagnéticas sempre vão obdecer as equações de Maxwell e suas condições de contorno.
Parâmetros considerados no Fenômeno de Reflexão e Refração:
- Características do meio 1 e meio 2: Condutividade Elétrica, permissividade elétrica, permeabilidade magnética.
- Ângulo da onda incidente \phi_i, ângulo da onda refletida \phi_r, e o ângulo da onda transmitida ou refratada \phi_t. Os ângulos são em relação a normal.
- Polarização da Onda incidente.
OBS: Assume-se que a fonte de onda eletromagnética tem uma distância suficiente para tal fenômeno. Em forma menos formal, podemos dizer que a fonte de onda está bem “longe”.
Vetores de Propagações no Estudo da Reflexão e Refração
Relembrando que o vetor de propagação descreve a direção, orientação e a velocidade que uma onda eletromagnética tem enquanto se propaga em um meio onde possui suas características próprias.
Uma vez que temos uma onda incidente atingindo uma interface entre meios, e como produto disso surgindo uma onda refletida e uma onda transmitida (ou refratada), teremos então, três vetores de propagação:
\vec{\gamma}_i \to vetor propagação incidente\vec{\gamma}_r \to vetor propagação refletida\vec{\gamma}_t \to vetor propagação transmitidaAs Ondas que serão estudadas são Harmônicas no Tempo:
Portanto, as ondas assumem o seguinte comportamento algebrico (A equação de Helmholtz – Solução geral da onda eletromagnética).
\large{\vec{A} = \vec{A_o}.e^{-\vec{\gamma}. \vec{r}}}
Essa equação portanto descreve as ondas eletromagneticas de ponto a ponto, sendo que um ponto em qualquer ponto do espaço em coordenadas cartesianas é dada por:
\large{\vec{r} = x.\hat{x} + y.\hat{y} + y.\hat{y}}
E podemos considerar uma solução particular, no qual z = 0, sem qualquer prejuizo matematico e, ou físico onde o plano tangente torna-se:
\large{\vec{r_s} = x.\hat{x} + y.\hat{y}}
A Composição de Ondas depois que atravessar de um meio a outro:
Assim, podemos descrever as ondas nesse fenômeno como:
IMPORTANTE: Vejamos que cada componente das ondas eletrômagnéticas (onda reletida, refratada e incidente) possui seu próprio vetor de propagação \vec{\gamma} .
E visto anteriormente que em todo campo elétrico há um campo magnético associado a ele, e do mesmo jeito podemos acontece na relação de vice-versa.
Veja que a impedância intrinsica de H_I e H_R é o mesmo, uma vez que se encontram no mesmo meio, que no caso é o meio 1.