1. Introdução ao Teorema do Confronto

O Teorema do Confronto, um conceito fundamental em cálculo, oferece uma maneira engenhosa de determinar os limites de funções que são difíceis de analisar. Conhecido alternativamente como Teorema do Sanduíche ou Teorema do Espremimento.

Este princípio tem raízes profundas na história matemática e é crucial para a compreensão de conceitos avançados de cálculo.

Entendendo a Essência

Em sua essência, o Teorema do Confronto trata de ‘espremer’ uma função entre duas outras funções em um determinado intervalo. É como encontrar o comportamento de uma função à medida que se aproxima de um ponto específico, confinando-a dentro dos limites de duas outras funções mais fáceis de avaliar.

Os exemplos desse artigo deixarão o teorema do confronto mais claro.

Perspectiva Histórica

O teorema, embora pareça moderno, tem suas origens nos primeiros trabalhos de cálculo. Ele incorpora o rigor e os fundamentos lógicos que matemáticos como Isaac Newton e Gottfried Wilhelm Leibniz estabeleceram. Este teorema é um testemunho de suas contribuições para o cálculo infinitesimal.

Importância no Cálculo

No cálculo, os limites são cruciais para entender o comportamento das funções em pontos específicos, especialmente onde não são explicitamente definidos. O Teorema do Confronto entra em jogo como uma ferramenta estratégica para avaliar esses limites, tornando-se um conceito fundamental para estudantes e profissionais.

2. Estrutura Conceitual do Teorema do Confronto

Nesta seção, mergulhamos no quadro conceitual do Teorema do Confronto, explorando seu princípio básico e seu papel fundamental na avaliação de limites em cálculo.

Princípio Básico do Teorema do Confronto

O Teorema do Confronto opera em um princípio simples, porém profundo: se uma função f(x) está sempre presa entre duas outras funções g(x) e h(x) que convergem para o mesmo limite em um determinado ponto,

então f(x) também deve convergir para esse mesmo limite nesse ponto. Esse princípio é semelhante a espremer um material entre duas superfícies sólidas; o material não tem outra opção a não ser se conformar com a pressão exercida.

Visualizando o Confronto

Imagine três linhas em um gráfico: a linha superior representa h(x), a linha inferior representa g(x) e a linha no meio é f(x). À medida que essas linhas se aproximam de um certo ponto no eixo x, g(x)

e h(x) se aproximam, espremendo f(x) entre elas. Se g(x) e h(x) se encontram em um ponto, f(x) é compelida a encontrar-se no mesmo ponto.

Papel do Teorema do Confronto na Avaliação de Limites

Limites em cálculo são frequentemente sobre se aproximar de um valor específico sem necessariamente alcançá-lo. O Teorema do Confronto é particularmente útil quando lidar diretamente com o limite de uma função é desafiador. Ele fornece uma maneira de determinar

3. Fundamento Matemático e Prova do Teorema do Confronto

A prova matemática do Teorema do Confronto é elegante e profunda, fornecendo uma demonstração clara de sua validade. Nesta seção, quebramos a prova do teorema em etapas compreensíveis, aprimorando sua compreensão deste importante conceito de cálculo.

Declaração Formal

O Teorema do Confronto é formalmente declarado da seguinte forma: Suponha que temos três funções, f(x), g(x) e h(x), e um ponto c. Se para todos x em um intervalo ao redor de c (exceto possivelmente no próprio c), g(x) ≤ f(x) ≤ h(x) for verdadeiro, e se os limites de g(x) e h(x) quando x se aproxima de c são os mesmos, então o limite de f(x) quando x se aproxima de c também é o mesmo.

Decompondo a Prova

1. Preparando o Palco:
   • Assuma que g(x) ≤ f(x) ≤ h(x) perto do ponto a.
   • Assuma que lim_{x \to a} g(x) = L e lim_{x \to a} h(x) = L.
2. Entendendo as Desigualdades:
   • As desigualdades implicam que f(x) está encurralada entre g(x) e h(x).
   • À medida que x se aproxima do ponto x = a, f(x) é espremida.
   • se g(x) e h(x) convergirem para o mesmo limite.
   • f(x) terá de ter o mesmo valor que g(x) e h(x)!
3. Concluindo a Prova:
   • Como f(x) está presa entre g(x) e h(x), e ambos g(x) e h(x) se aproximam de L, f(x) também deve

se aproximar de L.

Portanto: \boxed{lim_{x \to a} f(x) = L}

A Essência Lógica

A beleza dessa prova reside em sua simplicidade lógica. Ela utiliza elegantemente o conceito de limites e confinamento para deduzir o comportamento de uma função. Essa prova não apenas estabelece o teorema, mas também reforça os princípios fundamentais de limite e convergência em cálculo.

4. Como Aplicar o Teorema do Confronto

Aplicar o Teorema do Confronto em problemas de cálculo pode transformar um cálculo de limite aparentemente complicado em algo gerenciável. Esta seção orienta você pelos passos para usar efetivamente este teorema.

Passos para Aplicação

1. Identifique a Função Alvo:
   • Comece identificando a função f(x) cujo limite você precisa avaliar à medida que x se aproxima de um valor específico.
2. Encontre as Funções de Limitação:
   • Selecione duas funções, g(x) e h(x), de forma que g(x) ≤ f(x) ≤ h(x) para todos x próximos ao ponto de interesse, exceto possivelmente no próprio ponto.
3. Verifique a Convergência dos Limites:
   • Garanta que ambas g(x) e h(x) convergem para o mesmo limite conforme x se aproxima do valor alvo. Isso é crucial para a aplicação do teorema.
4. Aplique o Teorema:
   • Se as condições forem atendidas, conclui-se que: lim_{x \to a} g(x) = lim_{x \to a} f(x) = lim_{x \to a} h(x)

Dicas Práticas para Aplicação Eficaz

• Escolha Funções de Limitação Apropriadas: Selecionar as funções de limitação corretas é fundamental. Elas devem ser mais simples do que f(x) e seus limites mais fáceis de calcular.
• Use Análise Gráfica: Às vezes, traçar os gráficos das funções pode fornecer um entendimento mais claro de como elas se comportam perto do ponto de interesse e se efetivamente “espremem” a função alvo.
• Atenção ao Domínio: Garanta que as desigualdades sejam válidas em um intervalo em torno do ponto, mesmo que não sejam no próprio ponto.

Cenários Comuns

• Funções Trigonométricas: O Teorema do Confronto é frequentemente usado com funções trigonométricas, onde o cálculo direto do limite pode ser complexo.
• Funções Oscilantes: É particularmente útil para funções que oscilam perto do ponto de interesse, pois podem ser limitadas por funções mais simples.

Exemplo: Ilustrando o Teorema

Imagine um cenário onde você precisa encontrar lim_{x→0} x^2 sin(1/x). Aqui, você pode usar o Teorema do Confronto limitando a função com -x^2 ≤ x^2 sin(1/x) ≤ x^2, e então mostrar que ambos os limites convergem para 0 conforme x se aproxima de 0.

5. Teorema do Confronto na Prática: Exercícios Resolvidos

O Teorema do Confronto não é apenas um conceito teórico; ele tem aplicações práticas em vários cenários. Esta seção fornece exemplos do mundo real que ilustram a utilidade do teorema na solução de problemas de cálculo.

Exemplo 1: Limites Trigonométricos

Problema: Verifique o limite de sin(x)/x à medida que x se aproxima de 0.

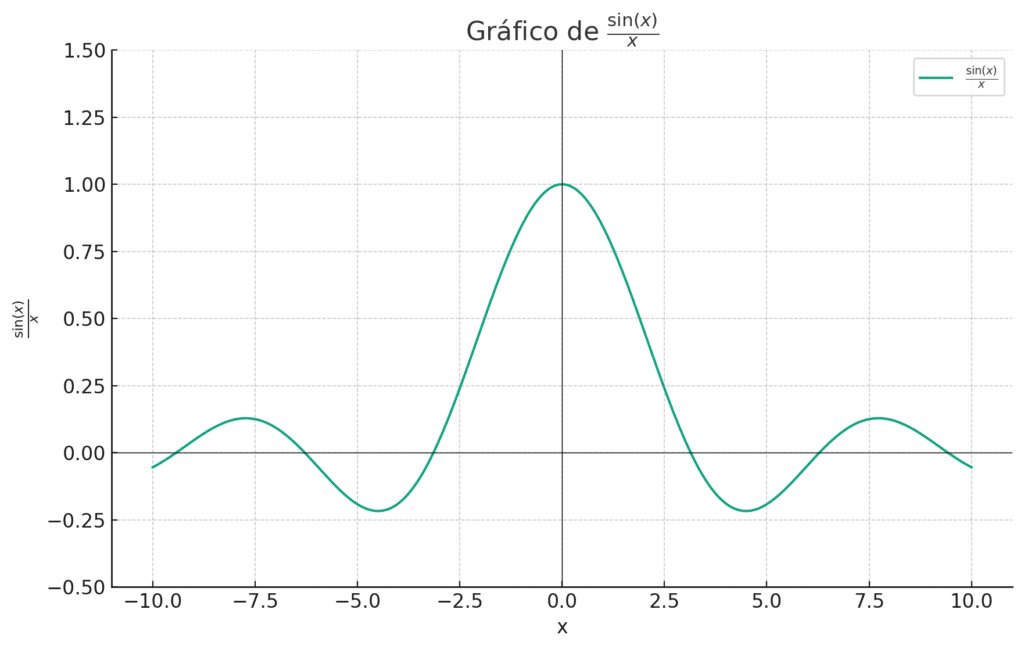
Ainda não vamos provar algebricamente nesse artigo. Mas lembre-se desse limite, pois este é considerado um limite fundamental e muito cobrado nas provas de cálculo diferencial e integral I.

lim_{(x \to 0)}\frac{sen(x)}{x} = 1

Exemplo 2: Funções Oscilantes

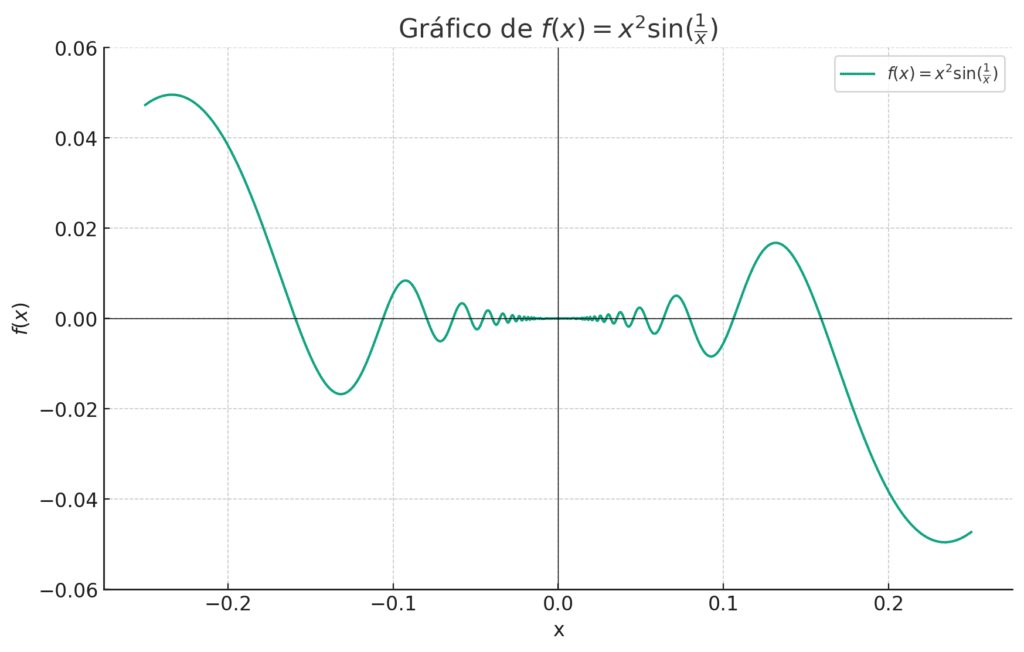
Problema: Avalie o limite de x^2 sin(1/x) à medida que x se aproxima de 0.

Se utilizarmos a propriedade do produto de limites veriamos que:

lim_{x \to 0} F(x) = [lim_{x \to 0}(x^2)]*[lim_{x \to 0}sen(1/x)]

Porém o limite em seno com seu ângulo dividido por 0 não existe. Portanto temos que apelar para o teorema do confronto.

Inicialmente vamos analisar os valores de seno:

Sabemos que sen(x) varia entre [-1,+1]; Na verdade independente do que estiver dentro dos parentesis em seno sempre vai variar entre [-1, +1] Portanto:

-1  \leq  sen{\frac{1}{x}} \leq +1

Multiplicando todos os lados por x² temos:

-x^2  \leq  x^2*sen{\frac{1}{x}} \leq x^2

Se tirarmos os limites dos valores do lado esquerdo e direito da inequação temos:

lim_{x \to 0}{(-x^2)}  \leq lim_{x \to 0} (x^2*sen{\frac{1}{x}}) \leq lim_{x \to 0}{(x^2)}

Portanto:

0  \leq  lim_{x \to 0}(x^2*sen{\frac{1}{x}}) \leq  0

Chegamos ao teorema do confronto! Ou seja se os limites existem e tendem ao valor L, nesse caso vale 0, temos que o limite do meio também vale 0.

Importante: Veja essa imagem abaixo para entender o ‘sanduiche’ que as funções -x² e x² fazem com sen(1/x):

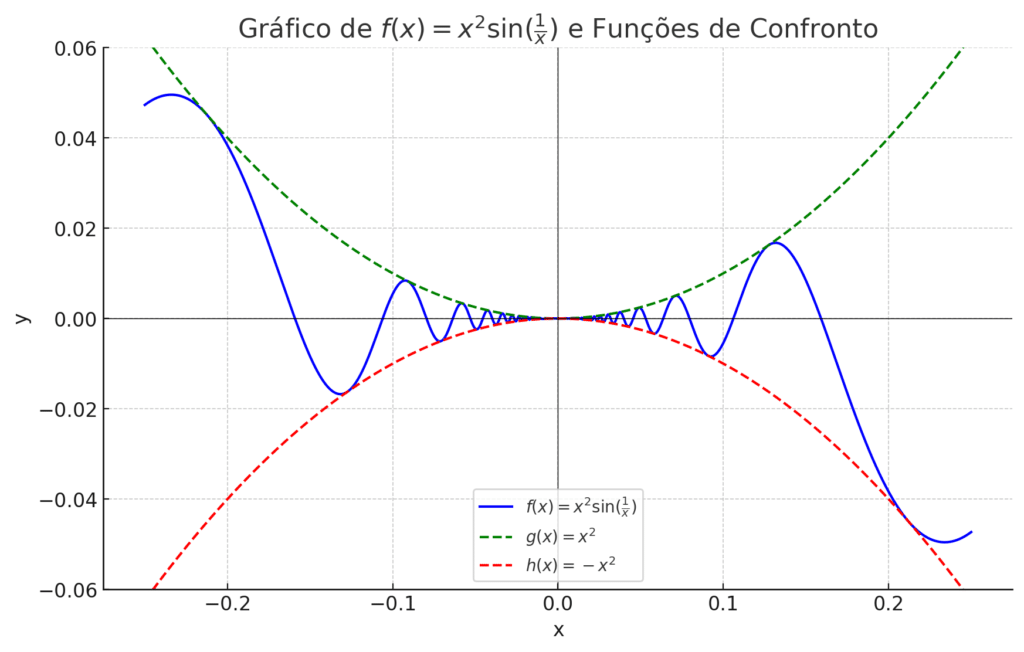
Assim concluimos que:

\boxed{lim_{x \to 0}(x^2*sen{\frac{1}{x}}) =  0}

Exemplo 3: Limites Polinomiais

Problema: Encontre o limite de x^4 sin(x) à medida que x se aproxima de 0.

A função seno, sin(x), varia entre -1 e +1 para qualquer valor de x. Assim, temos a desigualdade:

-1 \leq \sin(x) \leq +1

Multiplicando todos os termos por x^4, que é sempre positivo ou zero, mantemos a desigualdade:

-x^4 \leq x^4 \sin(x) \leq x^4

Agora, aplicamos o limite quando x quando tende a 0 em todos os termos da desigualdade:

\lim_{{x \to 0}} (-x^4) \leq \lim_{{x \to 0}} (x^4 \sin(x)) \leq \lim_{{x \to 0}} (x^4)

Veja que os limites serão zero do termo direito e esquerdo. A desigualdade nos mostra que x^4.sen(x) está entre 0 e 0 no caso. Qual valor que ele deve ter então? 0!

0 \leq \lim_{{x \to 0}} (x^4 \sin(x)) \leq 0

Pelo Teorema do Confronto, concluímos que:

 lim_{x \to 0} [x^4.sen(x)]= 0 

Compreendendo Através da Visualização

Estes exemplos podem ser melhor entendidos através da representação gráfica. Os gráficos das funções e seus limites ilustram como a função alvo é “espremida” e se aproxima de um limite.

O Quadro Mais Amplo

O Teorema do Confronto é particularmente útil em campos como física e engenharia, onde os limites de funções desempenham um papel crucial na modelagem e análise. Ele ajuda a entender comportamentos em pontos que não são facilmente acessíveis por métodos padrão.

6. Conceitos Errôneos Comuns e Desafios

O Teorema do Confronto é uma ferramenta poderosa em cálculo, mas não está livre de equívocos e desafios. Entender esses obstáculos comuns pode ajudar a aplicar o teorema de forma mais eficaz.

Equívoco 1: Sempre Aplicável

• Realidade: O Teorema do Confronto não é uma solução universal. Requer condições específicas para ser aplicado, principalmente, a função deve ser efetivamente ‘espremida’ entre duas funções de limitação sobre um certo intervalo.

Equívoco 2: Apenas para Funções Trigonométricas

• Realidade: Embora seja frequentemente usado para funções trigonométricas, o Teorema do Confronto se aplica a qualquer função, incluindo polinômios e funções oscilantes, desde que as condições sejam atendidas.

Desafio 1: Selecionar Funções de Limitação Apropriadas

• Problema: Um dos maiores desafios é escolher as funções de limitação corretas. Elas devem ser mais simples do que f(x) e seus limites mais fáceis de calcular.
• Solução: Um entendimento profundo do comportamento e características da função é crucial. Análise gráfica pode frequentemente fornecer insights sobre funções de limitação adequadas.

Desafio 2: Verificar as Condições

• Problema: Garantir que as funções de limitação convergem para o mesmo limite pode ser complicado, especialmente em cenários complexos.
• Solução: Análise cuidadosa e às vezes manipulação algébrica adicional são necessárias para confirmar que as condições do teorema são satisfeitas.

Desafio 3: Interpretar Erroneamente os Gráficos

• Problema: A interpretação incorreta ou plotagem inadequada das funções pode levar a conclusões incorretas.
• Solução: Prática e experiência, juntamente com a verificação cruzada usando diferentes métodos, podem ajudar a melhorar a precisão na interpretação de gráficos.

Dicas para Superar Desafios

• Desenvolva uma Base Sólida: Um entendimento sólido de limites e comportamento de funções é crucial.
• Pratique com Variedade: Trabalhar em diversos problemas para se familiarizar com diferentes aplicações do teorema.
• Busque Feedback: Discutir problemas com colegas ou instrutores pode oferecer novas perspectivas e insights.

7. Representação Gráfica e Análise

Auxílios visuais desempenham um papel crucial na compreensão e aplicação do Teorema do Confronto. Gráficos não só oferecem uma imagem clara do comportamento das funções, mas também ajudam na identificação de funções de limitação apropriadas.

O Poder da Representação Gráfica

• Clareza: Gráficos oferecem uma representação visual de como a função alvo está sendo ‘espremida’ entre as funções de limitação, tornando mais fácil entender o conceito.
• Verificação: Eles servem como uma ferramenta para verificar se as funções de limitação convergem para o mesmo limite, um requisito chave do Teorema do Confronto.

Passos para Análise Gráfica Eficaz

1. Trace as Funções: Comece plotando a função alvo f(x) e as potenciais funções de limitação g(x) e h(x).
2. Identifique o Intervalo: Concentre-se no intervalo ao redor do ponto de interesse. É aqui que o ‘espremimento’ deve ocorrer.
3. Observe o Comportamento: Observe onde as funções convergem e quão estreitamente f(x) está contida dentro de g(x) e h(x).
4. Verifique a Convergência: Garanta que g(x) e h(x) convergem para o mesmo limite conforme x se aproxima do ponto de interesse.

Exemplo: Visualizando o Teorema do Confronto

Considere o exemplo de f(x) = x^2 sin(1/x). Traçar esta função junto com seus limites -x^2 e x^2 à medida que x se aproxima de 0 demonstra visualmente como f(x) é espremida e se aproxima do limite 0 (Visto na imagem do exercícios resolvidos)

Dicas para Análise Gráfica

• Use Tecnologia: Aproveite calculadoras gráficas ou software para traçar com precisão.
• Verificação Cruzada Analítica: Confirme suas descobertas gráficas com métodos analíticos para garantir precisão.
• Experimente com Diferentes Funções: Testar várias funções pode proporcionar percepções mais profundas e fortalecer seu entendimento da aplicação do teorema.

8. O Teorema do Confronto Além da Matemática

A aplicação do Teorema do Confronto estende-se para além do domínio da matemática pura, desempenhando um papel significativo em campos como física e engenharia. Esta seção explora seu impacto mais amplo e aplicações no mundo real.

Aplicações em Física

• Modelagem de Fenômenos Físicos: Na física, o Teorema do Confronto é usado para modelar comportamentos de sistemas físicos sob condições limitantes. Por exemplo, ajuda na compreensão do comportamento limite de funções de onda na mecânica quântica, onde a avaliação direta é frequentemente desafiadora.
• Previsão de Comportamento Próximo a Singularidades: O teorema auxilia na previsão de como quantidades físicas se comportam à medida que se aproximam de pontos singulares, um cenário comum na física teórica.

Aplicações em Engenharia

• Análise Estrutural: Engenheiros frequentemente usam o Teorema do Confronto para analisar tensão e deformação em materiais nos seus limites, especialmente ao avaliar condições de fronteira.
• Processamento de Sinais: Na engenharia elétrica, o teorema é aplicado no processamento de sinais para entender o comportamento de sinais à medida que se aproximam de pontos específicos, o que é crucial para a transmissão e recepção precisas de dados.

Aplicações Computacionais

• Otimização de Algoritmos: Em ciência da computação, o Teorema do Confronto pode ser usado para otimizar algoritmos, particularmente em análise numérica e modelagem computacional, onde limites de funções desempenham um papel crucial.
• Análise de Dados: O teorema encontra aplicações em ciência de dados para entender tendências à medida que os pontos de dados convergem para um limite, auxiliando na previsão ou compreensão de padrões subjacentes.

9. Tópicos Avançados e Leitura Adicional

Para aqueles que desejam aprofundar seu entendimento do Teorema do Confronto e suas aplicações, explorar tópicos avançados e materiais adicionais de leitura pode ser extremamente benéfico. Esta seção destaca alguns aspectos complexos do teorema e sugere materiais para leitura adicional.

Explorando os Fundamentos Teóricos

• Teoremas de Limite em Análise: Compreender outros teoremas de limite em análise matemática pode fornecer um contexto mais amplo para o Teorema do Confronto, mostrando seu lugar dentro da estrutura maior do cálculo.
• Análise Não-Padrão: Para uma abordagem mais teórica, explorar a análise não-padrão pode oferecer insights sobre os infinitesimais, fornecendo uma perspectiva diferente sobre limites e convergência.

Aplicações Avançadas

• Equações Diferenciais: O Teorema do Confronto encontra sua aplicação avançada na solução de equações diferenciais, particularmente ao estabelecer a existência e unicidade de soluções.
• Análise Complexa: Explorar o teorema no âmbito da análise complexa pode ser esclarecedor, especialmente na compreensão do comportamento de funções complexas.

Recursos para Leitura Adicional

• Livros Texto: Livros de cálculo avançado frequentemente oferecem uma exploração mais aprofundada do Teorema do Confronto. Recomendo os seguinte autores: James Stwert e Guidorizzi.
• Artigos de Pesquisa: Para os academicamente inclinados, artigos de pesquisa que focam nas aplicações do Teorema do Confronto em várias áreas podem ser uma fonte rica de informações.
• Sites que eu Recomendo esse Artigo: Khan academy – teorema do confronto;

Considerações Finais

O Teorema do Confronto é um portal para o mundo rico e diversificado do cálculo e análise matemática. Seja você um estudante, pesquisador ou apenas alguém com um interesse aguçado em matemática, explorar este teorema em profundidade pode ser recompensador e esclarecedor.