Introdução à Equações de Variáveis Separáveis:

Este capítulo é dedicado a uma classe especial de equações diferenciais conhecida como “Equações de Variáveis Separaveis”.

As equações diferenciais são ferramentas matemáticas poderosas usadas para modelar e entender fenômenos físicos, biologicos, matemáticos e muito mais.

Vamos mergulhar neste tópico, explorando o conceito, sua aplicação em fenômenos físicos e exemplos práticos.

O Conceito de Equações de Variáveis Separáveis

Considerando f em função de x e g em função de y, uma equação diferencial é chamada de separável se puder ser escrita na forma:

\frac{dy}{dx} = f(x)g(y)

Esse tipo de equação diferencial pode ser separada. De um lado deixamos somente os componentes em y, do outro deixamos somente em função de x. Portanto uma equação diferencial de variáveis separaveis consegue consegue ficar da seguinte maneira:

\frac{dy}{g(y)} = f(x)dx

Agora podemos integrar a equação inteira. Assim ‘tiramos’ o operador diferencial dos dois lados da equação.

\int \frac{dy}{g(y)} = \int f(x)dx

A resolução dessas integrais e a utilização de algumas manipulçoes algebricas torna-se o método geral para encontrar a solução desse tipo especial de equação diferencial.

Exercícios Resolvidos de Equações de Variáveis Separáveis:

1) Considere a seguinte equação diferencial:

\frac{dy}{dx} = 3y

Descubra a solução para essa equação.

Podemos verificar que essa representa uma equação de variáveis separaveis. Pois:

\frac{dy}{y} = 3.dx

Agora integramos ambos os lados:

\int \frac{dy}{y} = \int 3.dx

Resultado:

ln|y| = 3x + c

De acordo com as propriedades exponenciais e logaritmicas:

\text{Propriedade 1: }e^{ln(a)} = a

\text{Propriedade 2: }e^{a+b} = e^{a} . e^{b}

Aplicando no resultado das integrais temos:

1. Deixando a equação com exponencial.
2. Utilizamos as propriedades denotadas logo acima.
3. Isolamos o y.

e^{ln|y|} = e^{3x + c}

y = \pm (e^{3x}.e^c)

\text{Vejamos que } e^c \text{ é uma constante também! Chamemos ela de K} 

Portanto a solução para essa equação diferencial é:

\boxed{y = \pm K.e^{3x}}

2) Considere a seguinte equação diferencial:

y' = \frac{2x}{y}

Descubra a solução para essa equação.

Lembre-se que y’ é a mesma coisa que dy/dx. É uma notação diferente, porém comumente utilizada.

y' = \frac{dy}{dx} = \frac{2x}{y}

Esse exercício tem o mesmo método de solução que o anterior. Vejamos que é padrão esse tipo de solução. Vamos lá.

Separando variáveis:

y.dy = 2x.dx

Integrando a equação inteira:

\int y.dy = \int 2x.dx

Desse modo:

\frac{y^2}{2} = x^2 + C

y^2 = 2x^2 + 2C \text{, onde 2C = K (é tudo constante...)}

A solução dessa equação diferencial é dado por:

\boxed{y = \pm \sqrt{2x^2 +K }}

3) Considere a seguinte equação diferencial:

\frac{dy}{dx} = \frac{cos(x)}{y^2}

Descubra a solução para essa equação.

A cada exercício eu irei resolve-los de forma mais direta, pois trata-se da mesma aplicação dos exercícios 1 e 2.

y^2.dy = cos(x).dx

\int y^2.dy = \int cos(x).dx

\frac{y^3}{3}= sen(x)+c

y^3 = 3.sen(x)+3c

y = \sqrt[3]{3.sen(x)+K}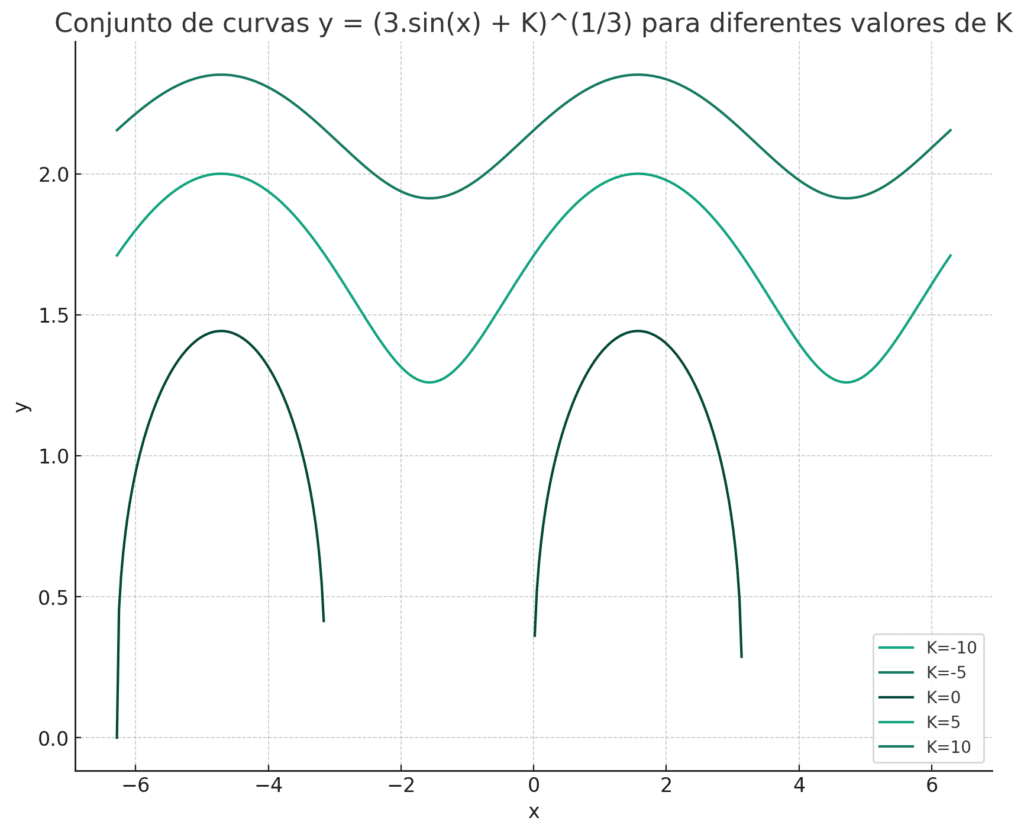

Exercícios Aprofundados:

4) (Boyce Diprima 6º Edição) Mostre que a esquação \frac{dy}{dx} = \frac{x^2}{1-y^2} é separável e depois encontre uma equação para suas curvas integrais.

Separando variáveis:

(1-y^2).dy = x^2.dx

Integrando a equação:

\int (1-y^2).dy =  \int x^2.dx

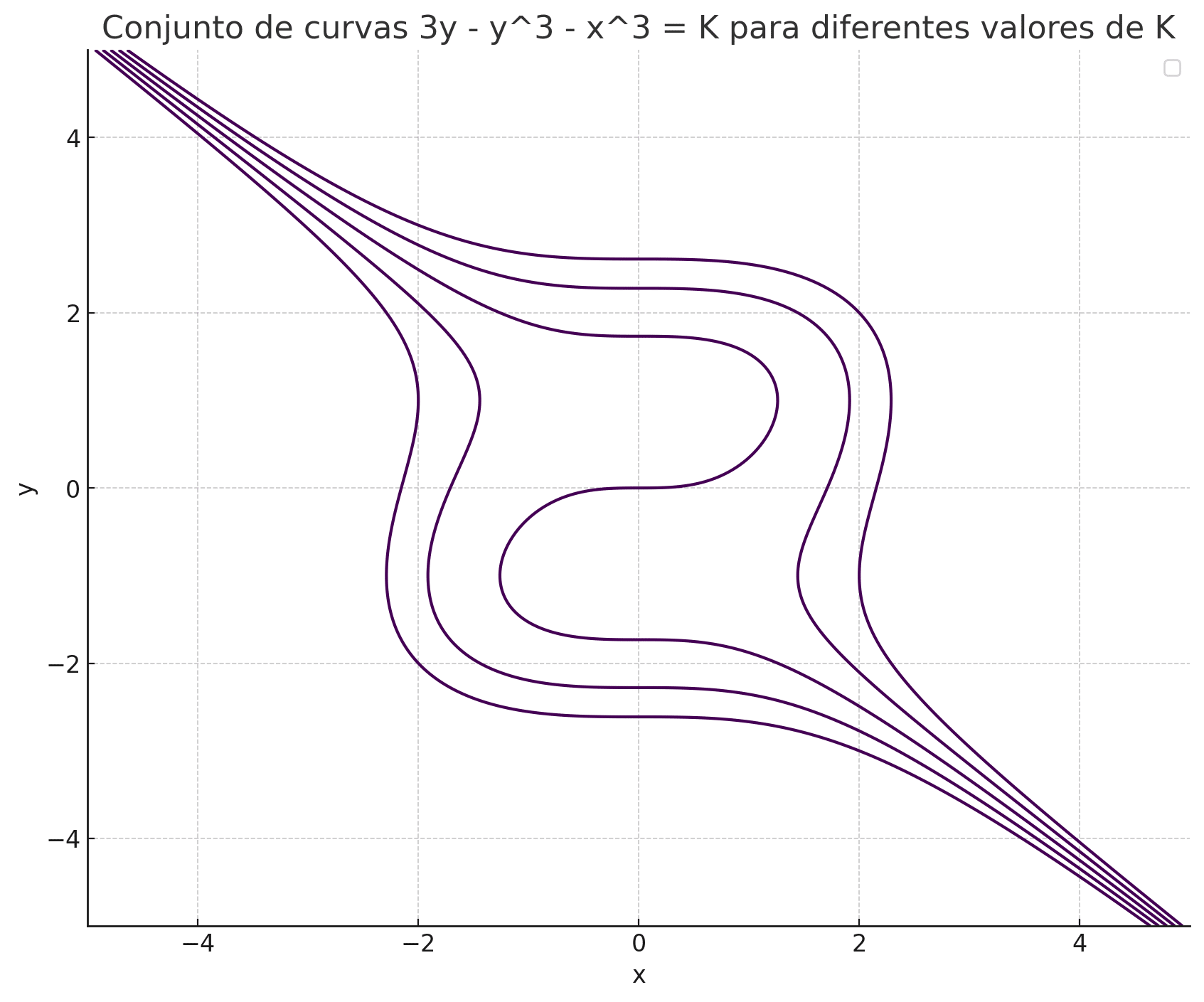
y - \frac{y^3}{3} = \frac{x^3}{3} +C

Desse modo, a curva que caracteriza uma solução geral da equação diferencial dada em questão:

\boxed{3y - y^3 - x^3 = K}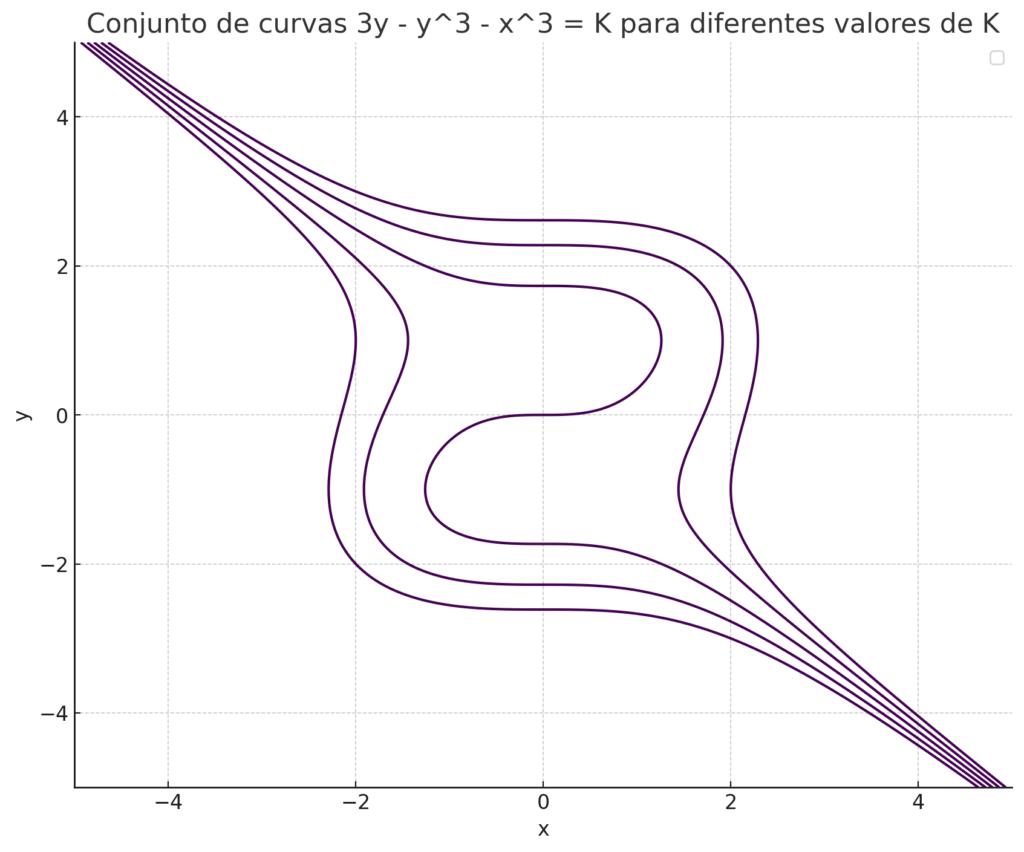

Teorema do Valor Inicial (PVI):

Trata-se de um problema no qual temos uma condição inicial dada.

Queremos resolver a seguinte equação diferencial de primeira ordem:

\frac{dy}{dt} = f(x,y)

E temos um condição pontual. Onde:

f(x_0) = y_0

Onde x_0 faz parte do intervalo I definido pela função.

O problema do valor inicial trata-se de uma solução da EDO, definida em algum intervalo I, onde a curva que é solução do problema passa pelo ponto inicial x_0

Exercícios Resolvidos: EDO’s Separáveis e PVI

5) (Boyce Diprima – 9ª Edição) Resolva o problema do valor inicial

\frac{dy}{dx} = \frac{3x^2 + 4x +2}{2(y-1)}

onde: y(0) = -1, e determine o intervalo no qual a solução existe.

O primeiro passo é determinar a solução da equação diferencial. Vamos utilizar o mesmo método dos exercícios anteriores. Separando as variáveis:

(3x^2 + 4x + 2)dx = (2y - 1)dy

Essa equação é de variáveis separáveis.

Integrando a equação inteira:

\int (3x^2 + 4x + 2)dx = \int (2y - 1)dy

x^3+2x^2+2x+c = y^3 -y

A solução da equação diferencial de forma explicita é:

x^3 + y^3 + 2x +y +c =0

Sabe-se que y = f(x) e também pelo enúnciado y(0) = -1

Desse modo, vamos aplicar o problema do valor inicial (PVI) na solução encontrada. Onde x = 0 e y =-1.

(0)^3 + (-1)^3 + 2.(0) + (-1) + c =0

Com o problema do valor inicial, conseguimos encontrar uma solução particular. Ou seja uma solução não generalizada com infinitos possíveis valores de c, mas uma solução particular onde c = 2.

c = 2

6) (Dennis G. Zill – 6ª Edição) Resolva o Problema do Valor Inicial:

\frac{dy}{dx}= -\frac{x}{y}

Onde y(4) = 3

Do mesmo jeito que foi resolvido o exercício 5:

-\int x.dx = \int y.dy

-x^2 + c = y^2

Reorganizando a equação:

x^2 + y^2 = c

Você reconhece essa equação? É a equação da circunferência. Onde r = \sqrt{c} e centro da circunferência está nas coordenadas (0,0).

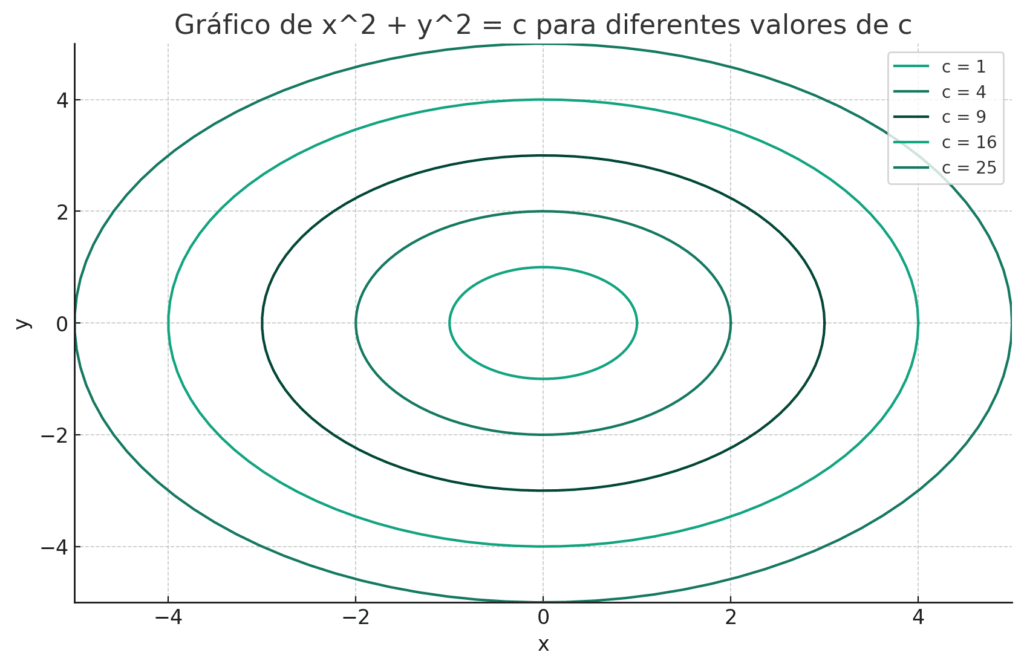
Aplicando o problema do valor inicial ( y=3, x=4):

3^2+4^2=c

c = 25

Portanto, uma circunferência de raio 5. Ou seja, com essa condição, sabemos que a solução única e particular é a circunferência de raio 5. O que traz à tona o que é o problema do valor inicial!

Aplicações em Fenômenos Físicos

As equações separáveis são amplamente utilizadas em vários campos da ciência e engenharia. Alguns exemplos incluem:

• Crescimento populacional
• Decaimento Radiativo
• Movimento de corpos sob resistência do ar

Esses exemplos mostram como manipular e resolver equações diferenciais separáveis usando apenas técnicas de álgebra e integração.

As equações separáveis são as mais simples de serem resolvidas nas equações diferenciais. Devido a sua simplicidade, os alunos tendem a substimar esse conteúdo, no qual é presente nos estudos posteriores de EDO’s. Não caia nesse erro!

Exercícios Aplicados e Aprofundados:

Equação de Variáveis Separáveis: Crescimento Populacional

7) (Boyce Diprima 10ª Edição – Cap 2. Ex.14) Suponha que determinada população tem uma taxa de crescimento que varia com o tempo e que essa população satisfaz a seguinte equação diferencial:

\frac{dy}{dt} = \frac{(0.5+sen(t)).y}{5}

a) Se y(0) = 1, encontre (ou estime) o instante \tau no qual a população dobrou. Escolha outras condicões iniciais e determine se o tempo de duplicação \tau depende da populacão inicial.
b) Suponha que a taxa de crescimento e substituida pelo seu valor medio 1/10. Determine o tempo de
duplicação \tau neste caso.
c) Suponha que o termo sen(t) na equação diferencial é substituido por sen(2 \pi t); ou seja, a variação na taxa de crescimento tem um frequência substancialmente alta. Que efeito isso tem no tempo de duplicação \tau?
d) Faca o grafico das solucties obtidas nos itens (a), (b) e (c) em um único conjunto de eixos;

Resposta:

a) Vejamos que a letra (a) é um problema de valor inicial (PVI) e Essa equação é de variáveis separáveis. Desse modo:

5\cdot\frac{dy}{y} = (0.5 +sen(t)).dt

5\int\frac{dy}{y} = \int(0.5 +sen(t)).dt

5.ln|y| = 0.5t -cos(t)+c

Pelas propriedades dadas no exercício 1. Podemos utilizar a operação inversa do logarítmo neperiano.

y = \pm(e^{0.1t-cos(t)+c/5})

O último termo da soma é constante de toda forma. Chamemos de K:

y = \mp K.cos(t).e^{0.1t}

Aplicando as condições iniciais:

1 = \pm K.cos(0).e^{(0.1\times0)}

1 = \pm K.cos(0).e^{0}

\boxed{\therefore K =\pm 1 }

A solução particular desse exercício é dado por:

y = \pm cos(t).e^{0.1t}

Estes exemplos mostram como os PVIs são essenciais para encontrar soluções específicas de equações diferenciais que são relevantes para situações reais. Ao aplicar a condição inicial, restringimos as infinitas soluções possíveis de uma equação diferencial para aquela que se adequa ao nosso problema específico.

Artigos Externos Recomendados:

https://pt.khanacademy.org/math/ap-calculus-ab/ab-differential-equations-new/ab-7-6/a/identifying-separable-equations

https://www.ime.unicamp.br/~valle/Teaching/2016/MA311/Aula2.pdf