Lei de Snell (Refração) para Meios Dielétricos

Conteúdos Anteriores:

Introdução:

Nessa aula, vamos ver como a lei de Snell (Refração) pode ser simplificada quando uma onda eletromagnética atravessa uma interface que divide dois meios dielétricos.

Muitos dos casos, a onda eletromagnética pode se propagar entre meios dielétricos. Ou seja, uma onda incidente se propaga no meio 1, dielétrico e sendo refratada (transferida) da interface até o meio 2 (outro dielétrico).

Veja a aula condutividade elétrica para relembrar o que caracteriza um meio/ e ou um material dielétrico. Porém em resumo temos geral, os dielétricos possuem condutividade elétrica extremamente baixa.

Portanto: $\sigma \to 0$

Mudanças na lei de Snell para Meios Dielétricos:

A lei de Snell foi definida na aula anterior do seguinte modo:

\therefore \boxed{\Large{\frac{sen\phi_i}{sen\phi_t} = \frac{\gamma_t}{\gamma_i}  =  \sqrt{\frac{\mu_2.(\sigma_2 + i\omega\epsilon_2)}{\mu_1 .(\sigma_1 + i\omega\epsilon_1)}}}}  \to   Lei   Descartes-Snell

Porém por ser meios dielétricos, vamos considerar que a condutividade elétrica é nula:

\therefore \Large{\frac{sen\phi_i}{sen\phi_t} = \frac{\gamma_t}{\gamma_i}  =  \sqrt{\frac{\mu_2.( 0 + i\omega\epsilon_2)}{\mu_1 .(0 + i\omega\epsilon_1)}}}

\therefore \Large{\frac{sen\phi_i}{sen\phi_t} = \frac{\gamma_t}{\gamma_i}  =  \sqrt{\frac{\mu_2. \cancel{i\omega}\epsilon_2}{\mu_1 . \cancel{i\omega}\epsilon_1}}}

Assim fica simplificado a lei da refração da seguinte forma:

\therefore (1)    \boxed{\large{\frac{sen\phi_i}{sen\phi_t} =  \sqrt{\frac{\mu_2. \epsilon_2}{\mu_1 . \epsilon_1}}}} \to Lei  de  Snell  para  meios  dielétricos.

Velocidade de Propagação das Ondas Eletromagnéticas:

A velocidade de propagação da onda eletromagnética em meios dielétricos, onde a condutividade elétrica é nula ou despresível, pode ser calculado a partir da formula abaixo:

\boxed{\large{ v = (\sqrt{\mu.\epsilon})^{-1}}}

ou expresso da forma abaixo:

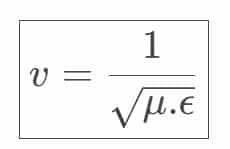
A lei de snell em função da velocidade em meios dielétricos fica do seguinte modo:

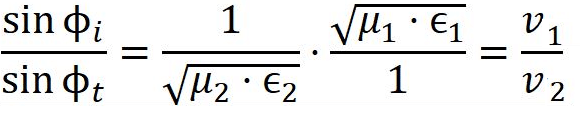
Lei de Snell em função de Índices de Refração:

Índice de Refração: É uma propriedade do material ou do meio no qual relaciona o comportamento da velocidade de propagação da onda eletromagnética com a velocidade da luz no vácuo. Representado pela letra N.

\boxed{\large{N = \frac{c}{v}}}

onde:

c = 3.10^8 m/s (velocidade da luz no vácuo)

v  \to  velocidade  da  luz  no  meio  em  questão

Portanto, enquanto menor a velocidade de propagação da onda em um certo meio, temos que o valor de N é maior.

Podemos agora fazer algumas manipulações algébricas na lei de Snell, de modo que ficará da seguinte forma:

$\Large{\frac{sen(\theta_i)}{sen(\theta_t) } = \frac{v_1}{v_2}}$

Podemos fazer a seguinte manipulação:

$\Large{\frac{sen(\theta_i)}{sen(\theta_t) } = \frac{v_1}{v_2}*\left(\frac{c}{c}\right)}$

Ajeitando a equação:

$\Large{\frac{sen(\theta_i)}{sen(\theta_t) } = \left(\frac{v_1}{c}\right)*\left(\frac{c}{v_2}\right)}$

Sabendo que $N_1 = \large{\frac{c}{v_1}}$ e $N_2 = \large{\frac{c}{v_2}}$ , podemos substituir na equação da seguinte forma:

\Large{\frac{sen(\theta_i)}{sen(\theta_t)  } = \left(\frac{N_2}{N_1}\right)}

chegando então à lei de Snell em função aos índices de refração:

\boxed{sen(\theta_i).N_1 = sen(\theta_t).N_2} \to Lei  de  Snell  em  função  dos  índices  de  refração